No CrossRef data available.
Article contents
Paths, tree homomorphisms and disequalities for 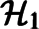
Published online by Cambridge University Press: 06 December 2017
Abstract
It is well known that satisfiability is decidable for Horn clauses of the class 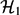 . Since arbitrary Horn clauses can naturally be approximated by
. Since arbitrary Horn clauses can naturally be approximated by 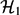 -clauses,
-clauses, 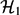 can be used for realizing any program analysis which can be specified by means of Horn clauses. Recently, we have shown that decidability for Horn clauses from
can be used for realizing any program analysis which can be specified by means of Horn clauses. Recently, we have shown that decidability for Horn clauses from 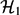 is retained if the clauses are either extended with tests for disequality between subterms identified by paths or for disequality between homomorphic images of terms. These two results refer to orthogonal extensions of
is retained if the clauses are either extended with tests for disequality between subterms identified by paths or for disequality between homomorphic images of terms. These two results refer to orthogonal extensions of 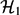 -clauses. Here, we provide a generalization of both results. For that, we introduce hom-path disequalities and show that for each finite set of
-clauses. Here, we provide a generalization of both results. For that, we introduce hom-path disequalities and show that for each finite set of 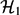 -clauses extended with such tests an equivalent tree automaton with hom-path disequalities can be constructed. Since emptiness for that class of automata has been shown decidable by Godoy et al. in 2010, we conclude that satisfiability is decidable for
-clauses extended with such tests an equivalent tree automaton with hom-path disequalities can be constructed. Since emptiness for that class of automata has been shown decidable by Godoy et al. in 2010, we conclude that satisfiability is decidable for 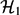 -clauses with hom-path disequalities.
-clauses with hom-path disequalities.
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 28 , Issue 10 , November 2018 , pp. 1786 - 1846
- Copyright
- Copyright © Cambridge University Press 2017
Footnotes
This work was partly supported by the DFG Graduiertenkolleg 1480 (PUMA).


