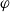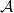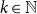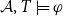1. Introduction
In this article, we study the parameterized complexity of weighted team definability for logics in team semantics. Team definability is a natural analog of the notion of Fagin-definability whose weighted version can be used to characterize the W-hierarchy in parameterized complexity (Downey et al. Reference Downey, Fellows and Regan1998). We give several results on the complexity of this problem for dependence, independence, and inclusion logic formulas.
The birth of the nowadays established logics of dependence and independence can be traced back to the introduction of dependence logic in 2007 (Väänänen Reference Väänänen2007). In team semantics, formulas are interpreted by sets of assignments (teams) instead of a single assignment as in Tarski’s semantics of first-order logic. Syntactically dependence logic extends first-order logic by new dependence atomic formulas (dependence atoms)
![]() ${\mathsf{dep}}({\mathbf{x}};{{y}})$
expressing that the values of variables
${\mathsf{dep}}({\mathbf{x}};{{y}})$
expressing that the values of variables
![]() $\mathbf x$
functionally determine the value of the variable y in the team under consideration. Independence and inclusion logics are further extensions of first-order logic by independence atoms
$\mathbf x$
functionally determine the value of the variable y in the team under consideration. Independence and inclusion logics are further extensions of first-order logic by independence atoms
![]() ${\mathbf{x}}\bot_{\mathbf{z}}\mathbf{y}$
and inclusion atoms
${\mathbf{x}}\bot_{\mathbf{z}}\mathbf{y}$
and inclusion atoms
![]() $\mathbf x \subseteq \mathbf y$
which essentially correspond to embedded multivalued dependences and inclusion dependences from database theory (Galliani Reference Galliani2012; Grädel and Väänänen Reference Grädel and Väänänen2013).
$\mathbf x \subseteq \mathbf y$
which essentially correspond to embedded multivalued dependences and inclusion dependences from database theory (Galliani Reference Galliani2012; Grädel and Väänänen Reference Grädel and Väänänen2013).
For the applications, it is important to understand the complexity theoretic aspects of team-based logics. During the past ten years, the expressivity and complexity theoretic aspects of logics in first-order (also propositional Yang and Väänänen Reference Yang and Väänänen2017, modal Hella et al. Reference Hella, Kuusisto, Meier and Virtema2019, Reference Hella, Kuusisto, Meier and Vollmer2020, temporal Gutsfeld et al. Reference Gutsfeld, Meier, Ohrem, Virtema, Baier and Fisman2022 and probabilistic Durand et al. Reference Durand, Hannula, Kontinen, Meier, Virtema, Ferrarotti and Woltran2018) team semantics have been studies extensively (see, e.g., Hannula et al. Reference Hannula, Kontinen, Virtema and Vollmer2018, Lück Reference Lück2019, Hannula et al. Reference Hannula, Kontinen, Van den Bussche and Virtema2020, Durand et al. Reference Durand, Kontinen, de Rugy-Altherre and Väänänen2022). The baseline for these studies is the well-known results stating that the sentences of dependence logic and independence logic are equivalent to existential second-order logic (Grädel and Väänänen Reference Grädel and Väänänen2013), while inclusion logic corresponds to positive greatest fixed point logic and thereby captures
![]() ${{\mathbf{P}}}$
over finite (ordered) structures (Galliani and Hella Reference Galliani, Hella and Della Rocca2013). In team semantics results for sentences of the logic do not immediately extend to open formulas. In particular, the open formulas of dependence logic correspond in expressive power to sentences of
${{\mathbf{P}}}$
over finite (ordered) structures (Galliani and Hella Reference Galliani, Hella and Della Rocca2013). In team semantics results for sentences of the logic do not immediately extend to open formulas. In particular, the open formulas of dependence logic correspond in expressive power to sentences of
![]() ${{\mathcal{ESO}}}$
with an extra relation encoding the team that occurs only negatively in the sentence (Kontinen and Väänänen Reference Kontinen and Väänänen2009). For independence logic, the requirement of negativity can be lifted (Galliani Reference Galliani2012). For inclusion logic an analogous result shows that any first-order sentence
${{\mathcal{ESO}}}$
with an extra relation encoding the team that occurs only negatively in the sentence (Kontinen and Väänänen Reference Kontinen and Väänänen2009). For independence logic, the requirement of negativity can be lifted (Galliani Reference Galliani2012). For inclusion logic an analogous result shows that any first-order sentence
![]() $\varphi(R)$
whose truth is preserved under R-unions can be expressed by an inclusion logic formula
$\varphi(R)$
whose truth is preserved under R-unions can be expressed by an inclusion logic formula
![]() $\varphi^*(\mathbf x)$
. In other words, for all
$\varphi^*(\mathbf x)$
. In other words, for all
![]() $\mathcal{A}$
and teams
$\mathcal{A}$
and teams
![]() $T\neq \emptyset$
:
$T\neq \emptyset$
:
where
![]() $\mathrm{rel}(T)$
is a relation encoding the team T (Galliani and Hella Reference Galliani, Hella and Della Rocca2013). These results can be used to relate weighted team definability to weighted Fagin-definablity. However, it is instructive to note that, due to higher expressive power of the logics considered in this article, the syntactic complexity of a formula does not in general correlate with the complexity of the model-checking of the formula. In particular, any formula of dependence and independence logic is logically equivalent to a formula with
$\mathrm{rel}(T)$
is a relation encoding the team T (Galliani and Hella Reference Galliani, Hella and Della Rocca2013). These results can be used to relate weighted team definability to weighted Fagin-definablity. However, it is instructive to note that, due to higher expressive power of the logics considered in this article, the syntactic complexity of a formula does not in general correlate with the complexity of the model-checking of the formula. In particular, any formula of dependence and independence logic is logically equivalent to a formula with
![]() $\forall\exists$
-quantifier prefix (Väänänen Reference Väänänen2007, Theorem 6.15) (Kontinen and Väänänen Reference Kontinen and Väänänen2009, Theorem 4.9).
$\forall\exists$
-quantifier prefix (Väänänen Reference Väänänen2007, Theorem 6.15) (Kontinen and Väänänen Reference Kontinen and Väänänen2009, Theorem 4.9).
A formalism to enhance the understanding of the inherent intractability of computational problems is brought by the framework of parameterized complexity (Downey and Fellows Reference Downey and Fellows2013). Here, one aims to find parameters relevant for practice allowing to solve the problem by algorithms running in time
![]() $f(k)\cdot n^{O(1)}$
, for some computable function f, where k is the parameter value and n is the input length. Problems with such a running time are called fixed-parameter tractable (
$f(k)\cdot n^{O(1)}$
, for some computable function f, where k is the parameter value and n is the input length. Problems with such a running time are called fixed-parameter tractable (
![]() ${{\mathbf{FPT}}}$
) and correspond to efficient computation in the parameterized setting. The problems solvable within the runtimes of the form
${{\mathbf{FPT}}}$
) and correspond to efficient computation in the parameterized setting. The problems solvable within the runtimes of the form
![]() $f(k)\cdot n^{O(1)}$
with respect to nondeterministic machines belong to the complexity class
$f(k)\cdot n^{O(1)}$
with respect to nondeterministic machines belong to the complexity class
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}\supseteq{{\mathbf{FPT}}}$
. Moreover, restricting the amount of nondeterminism allows to study a subclass
${{\mathbf{para}}}{{\mathbf{NP}}}\supseteq{{\mathbf{FPT}}}$
. Moreover, restricting the amount of nondeterminism allows to study a subclass
![]() ${{\mathbf{W}[{{\mathbf{P}}}]}}\subseteq {{\mathbf{para}}}{{\mathbf{NP}}}$
. The complexity class
${{\mathbf{W}[{{\mathbf{P}}}]}}\subseteq {{\mathbf{para}}}{{\mathbf{NP}}}$
. The complexity class
![]() ${{\mathbf{W}[{{\mathbf{P}}}]}}$
is defined via nondeterministic machines that have at most
${{\mathbf{W}[{{\mathbf{P}}}]}}$
is defined via nondeterministic machines that have at most
![]() $h(k)\cdot\log n$
many nondeterministic steps, where h is a computable function. In between
$h(k)\cdot\log n$
many nondeterministic steps, where h is a computable function. In between
![]() ${{\mathbf{FPT}}}$
and
${{\mathbf{FPT}}}$
and
![]() ${{\mathbf{W}[{{\mathbf{P}}}]}}$
, a presumably infinite
${{\mathbf{W}[{{\mathbf{P}}}]}}$
, a presumably infinite
![]() $\mathbf{W}$
-hierarchy is contained:
$\mathbf{W}$
-hierarchy is contained:
![]() ${{\mathbf{FPT}}}\subseteq{{\mathbf{W}[1]}}\subseteq{{\mathbf{W}[2]}}\subseteq\dots\subseteq{{\mathbf{W}[{{\mathbf{P}}}]}}$
. It is unknown whether any of these inclusions is strict. Showing
${{\mathbf{FPT}}}\subseteq{{\mathbf{W}[1]}}\subseteq{{\mathbf{W}[2]}}\subseteq\dots\subseteq{{\mathbf{W}[{{\mathbf{P}}}]}}$
. It is unknown whether any of these inclusions is strict. Showing
![]() ${{\mathbf{W}[1]}}$
-hardness of a problem in parameterized world intuitively corresponds to being intractable in this setting. Moreover,
${{\mathbf{W}[1]}}$
-hardness of a problem in parameterized world intuitively corresponds to being intractable in this setting. Moreover,
![]() ${{\mathbf{W}[1]}}$
contains problems that can be solved by an algorithm whose nondeterministic steps are bounded in terms of the parameter and occur at the end of the computation.
${{\mathbf{W}[1]}}$
contains problems that can be solved by an algorithm whose nondeterministic steps are bounded in terms of the parameter and occur at the end of the computation.
Our contributions. We define and study the parameterized complexity of weighted team definability with respect to formulas of several team-based logics. Moreover, we establish the relationship between our framework and the problem of weighted Fagin definability. In more details, we explore the complexity of weighted team definability in parameterized setting for dependence, independence, and inclusion logic formulas as well as sentences. Thereby, we prove and obtain novel logical characterizations of, and new complete problems for, the aforementioned central parameterized complexity classes, i.e., the
![]() ${{\mathbf{W}}}$
-hierarchy,
${{\mathbf{W}}}$
-hierarchy,
![]() ${{\mathbf{W}[{{\mathbf{P}}}]}}$
, and
${{\mathbf{W}[{{\mathbf{P}}}]}}$
, and
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
. Table 1 gives a partial overview of our results concerning weighted team definability.
${{\mathbf{para}}}{{\mathbf{NP}}}$
. Table 1 gives a partial overview of our results concerning weighted team definability.
Table 1. Partial overview of our results concerning weighted team definability with pointers to the respective theorem or corollary

Related work. The complexity of counting/enumerating satisfying teams for a fixed first-order formula of team-based logic has been studied before (Haak et al. Reference Haak, Kontinen, Müller, Vollmer and Yang2019, Reference Haak, Meier, Müller and Vollmer2022). Furthermore, there are also recent works on the parameterized complexity model-checking and satisfiability for propositional and first-order team-based logics (Kontinen et al. 2022;Mahmood andMeier Reference Mahmood and Meier2022; Mahmood and Virtema Reference Mahmood and Virtema2021; Meier and Reinbold Reference Meier and Reinbold2018). Regarding the descriptive complexity, Downey et al. (Reference Downey, Fellows and Regan1998) explored the logical characterization of the classes in the
![]() ${{\mathbf{W}}}$
-hierarchy.
${{\mathbf{W}}}$
-hierarchy.
2. Preliminaries
We require a basic knowledge of standard notions from classical complexity theory (Papadimitriou Reference Papadimitriou1994). The classical complexity classes we encounter mostly in this work are
![]() ${{\mathbf{P}}}$
and
${{\mathbf{P}}}$
and
![]() $ {{\mathbf{NP}}}$
together with their respective completeness notions, employing polynomial time many-one reductions (
$ {{\mathbf{NP}}}$
together with their respective completeness notions, employing polynomial time many-one reductions (
![]() ${{\leq^{{{\mathbf{P}}}}_m}}$
). Moreover, we assume the reader is familiar with the basic first-order (predicate) logic (Ebbinghaus and Flum Reference Ebbinghaus and Flum1995). In the following, we define a few important classes of first-order formulas that are relevant to the results in this work.
${{\leq^{{{\mathbf{P}}}}_m}}$
). Moreover, we assume the reader is familiar with the basic first-order (predicate) logic (Ebbinghaus and Flum Reference Ebbinghaus and Flum1995). In the following, we define a few important classes of first-order formulas that are relevant to the results in this work.
FO-Formula Classes. The class of all first-order formulas is denoted by
![]() ${{\mathcal{FO}}}$
. Let
${{\mathcal{FO}}}$
. Let
![]() $\tau$
be a relational vocabulary and
$\tau$
be a relational vocabulary and
![]() $R\in \tau$
be a relation symbol of arity r. An atomic formula is a formula of the form
$R\in \tau$
be a relation symbol of arity r. An atomic formula is a formula of the form
![]() $x = y$
or
$x = y$
or
![]() $R(x_1,\dots, x_r)$
. A literal is an atomic or a negated atomic formula. A quantifier-free formula is a formula that contains no quantifiers and a formula is in negation normal form (NNF) if the negation symbols occurs only front of atoms. A formula
$R(x_1,\dots, x_r)$
. A literal is an atomic or a negated atomic formula. A quantifier-free formula is a formula that contains no quantifiers and a formula is in negation normal form (NNF) if the negation symbols occurs only front of atoms. A formula
![]() $\varphi$
is in prenex normal form if
$\varphi$
is in prenex normal form if
![]() $\varphi$
has the form
$\varphi$
has the form
![]() $Q_1x_1\dots Q_nx_n \psi$
, where
$Q_1x_1\dots Q_nx_n \psi$
, where
![]() $\psi$
is quantifier free and
$\psi$
is quantifier free and
![]() $Q_1,\dots,Q_n\in\{\exists, \forall\}$
. The classes
$Q_1,\dots,Q_n\in\{\exists, \forall\}$
. The classes
![]() ${{\mathrm{\Sigma}_{0}}}$
and
${{\mathrm{\Sigma}_{0}}}$
and
![]() ${{\mathrm{\Pi}_{0}}}$
both consist of quantifier-free formulas. Then, for
${{\mathrm{\Pi}_{0}}}$
both consist of quantifier-free formulas. Then, for
![]() $t\geq 0 $
, the class
$t\geq 0 $
, the class
![]() ${{\mathrm{\Sigma}_{t+1}}}$
includes all formulas of the form
${{\mathrm{\Sigma}_{t+1}}}$
includes all formulas of the form
![]() $\exists x_1\dots \exists x_\ell \varphi$
, where
$\exists x_1\dots \exists x_\ell \varphi$
, where
![]() $\varphi\in {{\mathrm{\Pi}_{t}}}$
. Similarly,
$\varphi\in {{\mathrm{\Pi}_{t}}}$
. Similarly,
![]() ${{\mathrm{\Pi}_{t+1}}}$
includes all formulas of the form
${{\mathrm{\Pi}_{t+1}}}$
includes all formulas of the form
![]() $\forall x_1\dots \forall x_\ell \varphi$
, where
$\forall x_1\dots \forall x_\ell \varphi$
, where
![]() $\varphi\in {{\mathrm{\Sigma}_{t}}}$
.
$\varphi\in {{\mathrm{\Sigma}_{t}}}$
.
Fagin Definability. The first-order variables range over individual elements of the universe. In second-order logic, one also quantifies relation variables which range over relations on the universe. We now introduce first-order formulas where we also allow relation variables. Let
![]() $\tau$
be a vocabulary,
$\tau$
be a vocabulary,
![]() $X_i$
for
$X_i$
for
![]() $i\leq n$
be free relation variables of arity
$i\leq n$
be free relation variables of arity
![]() $s_i$
and
$s_i$
and
![]() $\varphi(X_1,\dots, X_n)$
be a
$\varphi(X_1,\dots, X_n)$
be a
![]() ${{\mathcal{FO}}}$
-formula with free relation variables in
${{\mathcal{FO}}}$
-formula with free relation variables in
![]() $\tau$
. Notice that
$\tau$
. Notice that
![]() $\varphi(X_1,\dots, X_n)$
does not contain free first-order variables. Moreover, let
$\varphi(X_1,\dots, X_n)$
does not contain free first-order variables. Moreover, let
![]() $\mathcal{A}$
be a
$\mathcal{A}$
be a
![]() $\tau$
-structure and
$\tau$
-structure and
![]() $S_i\subseteq A^{s_i}$
be relations over
$S_i\subseteq A^{s_i}$
be relations over
![]() $\mathcal{A}$
for
$\mathcal{A}$
for
![]() $i\leq n$
. Then we say that the tuple
$i\leq n$
. Then we say that the tuple
![]() $\bar S = (S_1,\dots,S_n)$
is a solution for
$\bar S = (S_1,\dots,S_n)$
is a solution for
![]() $\varphi$
in
$\varphi$
in
![]() $\mathcal{A}$
if
$\mathcal{A}$
if
![]() $\mathcal{A} \models \varphi(\bar S)$
. We call the following decision problem, the problem Fagin-defined by
$\mathcal{A} \models \varphi(\bar S)$
. We call the following decision problem, the problem Fagin-defined by
![]() $\varphi$
.
$\varphi$
.

Let
![]() ${{\mathrm{\Theta}}}\subseteq{{\mathcal{FO}}} $
be a class of formulas, then by
${{\mathrm{\Theta}}}\subseteq{{\mathcal{FO}}} $
be a class of formulas, then by
![]() $\mathrm{FD}\text-{{\mathrm{\Theta}}}$
we denote the class of all problems
$\mathrm{FD}\text-{{\mathrm{\Theta}}}$
we denote the class of all problems
![]() $\mathrm{FD}_\varphi$
such that
$\mathrm{FD}_\varphi$
such that
![]() $\varphi\in {{\mathrm{\Theta}}}$
. The following result regarding
$\varphi\in {{\mathrm{\Theta}}}$
. The following result regarding
![]() ${{\mathcal{FO}}}$
is known.
${{\mathcal{FO}}}$
is known.
Proposition 1. (Flum and Grohe Reference Flum and Grohe2006, Cor. 4.35).
![]() ${{\mathbf{NP}}} = \mathrm{FD}\text-{{\mathcal{FO}}} = \mathrm{FD}\text-{{\mathrm{\Pi}_{2}}}$
.
${{\mathbf{NP}}} = \mathrm{FD}\text-{{\mathcal{FO}}} = \mathrm{FD}\text-{{\mathrm{\Pi}_{2}}}$
.
Next we introduce the following weighted version of Fagin definabilty, where we restrict our solution to have a specific size for a single free relation symbol S of arity s. Notice that the inclusion of a single free relation variable is without loss of generality as allowing more than one such variables does not increase the complexity (see Flum and Grohe Reference Flum and Grohe2006, p.87).

As before, for a class
![]() ${{\mathrm{\Theta}}}\subseteq{{\mathcal{FO}}} $
of formulas, we denote by
${{\mathrm{\Theta}}}\subseteq{{\mathcal{FO}}} $
of formulas, we denote by
![]() $\mathrm{WD}\text-{{\mathrm{\Theta}}}$
the class of all problems
$\mathrm{WD}\text-{{\mathrm{\Theta}}}$
the class of all problems
![]() $\mathrm{WD}_\varphi$
such that
$\mathrm{WD}_\varphi$
such that
![]() $\varphi\in {{\mathrm{\Theta}}}$
.
$\varphi\in {{\mathrm{\Theta}}}$
.
Example 2. We assume standard graph theoretic notation and consider loop-free graphs. The problem![]() is defined as follows. Given a graph
is defined as follows. Given a graph
![]() $\mathcal{G}\mathrel{\mathop:}= (V,E)$
and
$\mathcal{G}\mathrel{\mathop:}= (V,E)$
and
![]() $k\in \mathbb N$
. Is there a set
$k\in \mathbb N$
. Is there a set
![]() $S\subseteq V$
such that
$S\subseteq V$
such that
![]() $|S|=k$
and
$|S|=k$
and
![]() $(u,v)\in E$
for every
$(u,v)\in E$
for every
![]() $x,y\in S$
? Then
$x,y\in S$
? Then![]() is
is
![]() $\mathrm{WD}_{\varphi_c}$
, where
$\mathrm{WD}_{\varphi_c}$
, where
Consequently,![]() is in
is in
![]() $\mathrm{WD}\text-{{\mathrm{\Pi}_{1}}}$
.
$\mathrm{WD}\text-{{\mathrm{\Pi}_{1}}}$
.
Moreover, Let![]() be the problem to determine if a graph
be the problem to determine if a graph
![]() $\mathcal{G}$
contains a set
$\mathcal{G}$
contains a set
![]() $S\subseteq V$
such that
$S\subseteq V$
such that
![]() $|S|=k$
and every vertex in
$|S|=k$
and every vertex in
![]() $V\setminus S$
is incident to some vertex in S? Then
$V\setminus S$
is incident to some vertex in S? Then ![]() is in
is in
![]() $\mathrm{WD}\text-{{\mathrm{\Pi}_{2}}}$
since the problem is
$\mathrm{WD}\text-{{\mathrm{\Pi}_{2}}}$
since the problem is
![]() $\mathrm{WD}_{\varphi_d}$
, where
$\mathrm{WD}_{\varphi_d}$
, where
Parameterized Complexity Theory. A parameterized problem (PP)
![]() $P\subseteq\Sigma^*\times\mathbb N$
is a subset of the cross-product of an alphabet and the natural numbers. For an instance
$P\subseteq\Sigma^*\times\mathbb N$
is a subset of the cross-product of an alphabet and the natural numbers. For an instance
![]() $(x,k)\in\Sigma^*\times\mathbb N$
, k is called the (value of the) parameter. A parameterization is a polynomial-time computable function that maps a value from
$(x,k)\in\Sigma^*\times\mathbb N$
, k is called the (value of the) parameter. A parameterization is a polynomial-time computable function that maps a value from
![]() $x\in\Sigma^*$
to its corresponding
$x\in\Sigma^*$
to its corresponding
![]() $k\in\mathbb N$
. The problem P is said to be fixed-parameter tractable (or in the class
$k\in\mathbb N$
. The problem P is said to be fixed-parameter tractable (or in the class
![]() ${{\mathbf{FPT}}}$
) if there exists a deterministic algorithm
${{\mathbf{FPT}}}$
) if there exists a deterministic algorithm
![]() $\mathcal A$
and a computable function f such that for all
$\mathcal A$
and a computable function f such that for all
![]() $(x,k)\in\Sigma^*\times \mathbb N$
, algorithm
$(x,k)\in\Sigma^*\times \mathbb N$
, algorithm
![]() $\mathcal A$
correctly decides the membership of
$\mathcal A$
correctly decides the membership of
![]() $(x,k)\in P$
and runs in time
$(x,k)\in P$
and runs in time
![]() $f(k)\cdot|x|^{O(1)}$
. The problem P belongs to the class
$f(k)\cdot|x|^{O(1)}$
. The problem P belongs to the class
![]() ${{\mathbf{XP}}}$
if
${{\mathbf{XP}}}$
if
![]() $\mathcal A$
runs in time
$\mathcal A$
runs in time
![]() $|x|^{f(k)}$
on a deterministic machine. Abusing a little bit of notation, we write
$|x|^{f(k)}$
on a deterministic machine. Abusing a little bit of notation, we write
![]() $\mathcal C$
-machine for the type of machines that decide languages in the class
$\mathcal C$
-machine for the type of machines that decide languages in the class
![]() $\mathcal C$
, and we will say a function f is
$\mathcal C$
, and we will say a function f is
![]() $\mathcal C$
-computable if it can be computed by a machine on which the resource bounds of the class
$\mathcal C$
-computable if it can be computed by a machine on which the resource bounds of the class
![]() $\mathcal C$
are imposed. The class
$\mathcal C$
are imposed. The class
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
includes problems decidable by a nondeterministic algorithm
${{\mathbf{para}}}{{\mathbf{NP}}}$
includes problems decidable by a nondeterministic algorithm
![]() $\mathcal A$
which runs in time
$\mathcal A$
which runs in time
![]() $f(k)\cdot|x|^{O(1)}$
for some computable function f. One can define a parameterized complexity class
$f(k)\cdot|x|^{O(1)}$
for some computable function f. One can define a parameterized complexity class
![]() ${{\mathbf{para}}}\mathcal C$
corresponding to a complexity class
${{\mathbf{para}}}\mathcal C$
corresponding to a complexity class
![]() $\mathcal C$
via a precomputation on the parameter.
$\mathcal C$
via a precomputation on the parameter.
Definition 3. Let
![]() $\mathcal C$
be any complexity class. Then
$\mathcal C$
be any complexity class. Then
![]() ${{\mathbf{para}}}\mathcal C$
is the class of all PPs
${{\mathbf{para}}}\mathcal C$
is the class of all PPs
![]() $P\subseteq\Sigma^*\times\mathbb N$
such that there exists a computable function
$P\subseteq\Sigma^*\times\mathbb N$
such that there exists a computable function
![]() $\pi\colon\mathbb N\to\Delta^*$
and a language
$\pi\colon\mathbb N\to\Delta^*$
and a language
![]() $L\in\mathcal C$
with
$L\in\mathcal C$
with
![]() $L\subseteq\Sigma^*\times\Delta^*$
such that for all
$L\subseteq\Sigma^*\times\Delta^*$
such that for all
![]() $(x,k)\in\Sigma^*\times\mathbb N$
we have that
$(x,k)\in\Sigma^*\times\mathbb N$
we have that
![]() $(x,k)\in P \Leftrightarrow (x,\pi(k))\in L$
.
$(x,k)\in P \Leftrightarrow (x,\pi(k))\in L$
.
Notice that
![]() ${{\mathbf{para}}}\mathbf{P}={{\mathbf{FPT}}}$
and the two definitions of
${{\mathbf{para}}}\mathbf{P}={{\mathbf{FPT}}}$
and the two definitions of
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
are equivalent.
${{\mathbf{para}}}{{\mathbf{NP}}}$
are equivalent.
A problem P is in the complexity class
![]() ${{\mathbf{W[P]}}}$
, if it can be decided by a NTM running in time
${{\mathbf{W[P]}}}$
, if it can be decided by a NTM running in time
![]() $f(k)\cdot|x|^{O(1)}$
steps, with at most g(k)-many nondeterministic steps, where f,g are computable functions. Moreover,
$f(k)\cdot|x|^{O(1)}$
steps, with at most g(k)-many nondeterministic steps, where f,g are computable functions. Moreover,
![]() ${{\mathbf{W[P]}}}$
is contained in the intersection of
${{\mathbf{W[P]}}}$
is contained in the intersection of
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
and
${{\mathbf{para}}}{{\mathbf{NP}}}$
and
![]() ${{\mathbf{XP}}}$
(for details see the textbook of Flum and Grohe Reference Flum and Grohe2006).
${{\mathbf{XP}}}$
(for details see the textbook of Flum and Grohe Reference Flum and Grohe2006).
Let
![]() $c\in\mathbb N$
and
$c\in\mathbb N$
and
![]() $P\subseteq\Sigma^*\times\mathbb N$
be a PP, then the c-slice of P, written as
$P\subseteq\Sigma^*\times\mathbb N$
be a PP, then the c-slice of P, written as
![]() $P_c$
is defined as
$P_c$
is defined as
![]() $P_c\:=\{\,(x,k)\in\Sigma^*\times\mathbb N\mid k=c\,\}$
. Notice that
$P_c\:=\{\,(x,k)\in\Sigma^*\times\mathbb N\mid k=c\,\}$
. Notice that
![]() $P_c$
is a classical problem then.
$P_c$
is a classical problem then.
Definition 4. Let
![]() $P\subseteq\Sigma^*\times\mathbb N,Q\subseteq\Gamma^*$
be two PPs. One says that P is fpt-reducible to Q,
$P\subseteq\Sigma^*\times\mathbb N,Q\subseteq\Gamma^*$
be two PPs. One says that P is fpt-reducible to Q,
![]() $P{{\leq^{{{\mathbf{FPT}}}}}} Q$
, if there exists an
$P{{\leq^{{{\mathbf{FPT}}}}}} Q$
, if there exists an
![]() ${{\mathbf{FPT}}}$
-computable function
${{\mathbf{FPT}}}$
-computable function
![]() $f\colon\Sigma^*\times\mathbb N\to\Gamma^*\times\mathbb N$
such that
$f\colon\Sigma^*\times\mathbb N\to\Gamma^*\times\mathbb N$
such that
-
for all
 $(x,k)\in\Sigma^*\times\mathbb N$
we have that
$(x,k)\in\Sigma^*\times\mathbb N$
we have that
 $(x,k)\in P\Leftrightarrow f(x,k)\in Q$
,
$(x,k)\in P\Leftrightarrow f(x,k)\in Q$
, -
there exists a computable function
 $g\colon\mathbb N\to\mathbb N$
such that for all
$g\colon\mathbb N\to\mathbb N$
such that for all
 $(x,k)\in\Sigma^*\times\mathbb N$
and
$(x,k)\in\Sigma^*\times\mathbb N$
and
 $f(x,k)=(x',k')$
we have that
$f(x,k)=(x',k')$
we have that
 $k'\leq g(k)$
.
$k'\leq g(k)$
.
Finally, in order to show that a problem P is
![]() ${{\mathbf{para}}}\mathcal C$
-hard for some complexity class
${{\mathbf{para}}}\mathcal C$
-hard for some complexity class
![]() $\mathcal C$
, it is sufficient to prove that for some
$\mathcal C$
, it is sufficient to prove that for some
![]() $c\in \mathbb N$
, the slice
$c\in \mathbb N$
, the slice
![]() $P_c$
is
$P_c$
is
![]() $\mathcal C$
-hard in the classical setting (Flum and Grohe Reference Flum and Grohe2006, Thm. 2.14).
$\mathcal C$
-hard in the classical setting (Flum and Grohe Reference Flum and Grohe2006, Thm. 2.14).
To define the complexity classes in
![]() ${{\mathbf{W}}}$
-hierarchy, the parameterized version of the problem
${{\mathbf{W}}}$
-hierarchy, the parameterized version of the problem
![]() $\mathrm{WD}_\varphi$
is now defined as follows.
$\mathrm{WD}_\varphi$
is now defined as follows.

The complexity classes of the
![]() ${{\mathbf{W}}}$
-hierarchy are characterized via the following definition.
${{\mathbf{W}}}$
-hierarchy are characterized via the following definition.
Definition 5. (Flum and Grohe Reference Flum and Grohe2006, Def. 5.1). For every
![]() $t\geq 1$
, we let
$t\geq 1$
, we let
![]() ${{\mathbf{W}[t]}}\mathrel{\mathop:}= [\text{p-}\mathrm{WD}\text-{{\mathrm{\Pi}_{t}}}]^{{{\mathbf{FPT}}}}$
. The class
${{\mathbf{W}[t]}}\mathrel{\mathop:}= [\text{p-}\mathrm{WD}\text-{{\mathrm{\Pi}_{t}}}]^{{{\mathbf{FPT}}}}$
. The class
![]() ${{\mathbf{W}[t]}}$
forms the t-th level of the
${{\mathbf{W}[t]}}$
forms the t-th level of the
![]() ${{\mathbf{W}}}$
-hierarchy.
${{\mathbf{W}}}$
-hierarchy.
Alternatively, the
![]() ${{\mathbf{W}}}$
-hierarchy can be defined via the weighted satisfiability problem for propositional formulas. Let I be a nonempty index set and
${{\mathbf{W}}}$
-hierarchy can be defined via the weighted satisfiability problem for propositional formulas. Let I be a nonempty index set and
![]() $d\in\mathbb N$
. Consider the following special subclasses of propositional formulas:
$d\in\mathbb N$
. Consider the following special subclasses of propositional formulas:
 $\begin{array}{@{}r@{\,}c@{\,}l@{}} \Gamma_{0, d} & =& \{\ell_1\land\dots\land \ell_c \mid \ell_1,\dots, \ell_c \text{ are literals and }c\leq d \},\\ \Delta_{0, d} & = & \{\ell_1\lor\dots\lor \ell_c \mid \ell_1,\dots, \ell_c \text{ are literals and }c\leq d \},\\ \Gamma_{t, d} & = & \left\{\,\bigwedge\limits_{i\in I} \alpha_i \,\middle|\, \alpha_i \in \Delta_{t-1,d} \text{ for } i \in I\, \right\}, \\ \Delta_{t, d} &= & \left\{\,\bigvee\limits_{i\in I} \alpha_i \,\middle|\, \alpha_i \in \Gamma_{t-1,d} \text{ for } i \in I\, \right\}.\end{array}$
$\begin{array}{@{}r@{\,}c@{\,}l@{}} \Gamma_{0, d} & =& \{\ell_1\land\dots\land \ell_c \mid \ell_1,\dots, \ell_c \text{ are literals and }c\leq d \},\\ \Delta_{0, d} & = & \{\ell_1\lor\dots\lor \ell_c \mid \ell_1,\dots, \ell_c \text{ are literals and }c\leq d \},\\ \Gamma_{t, d} & = & \left\{\,\bigwedge\limits_{i\in I} \alpha_i \,\middle|\, \alpha_i \in \Delta_{t-1,d} \text{ for } i \in I\, \right\}, \\ \Delta_{t, d} &= & \left\{\,\bigvee\limits_{i\in I} \alpha_i \,\middle|\, \alpha_i \in \Gamma_{t-1,d} \text{ for } i \in I\, \right\}.\end{array}$
Finally,
![]() $\Gamma^{+}_{t,d}$
(resp.
$\Gamma^{+}_{t,d}$
(resp.
![]() $\Gamma^{-}_{t,d}$
) denote the class of all positive (negative) formulas in
$\Gamma^{-}_{t,d}$
) denote the class of all positive (negative) formulas in
![]() $\Gamma_{t,d}$
.
$\Gamma_{t,d}$
.
The parameterized weighted satisfiability problem (
![]() $\text{p-} {{\mathrm{WSAT}}}$
) for propositional formulas is defined as below. The parameter weight of an assignment s is the number of variables mapped to 1 by s.
$\text{p-} {{\mathrm{WSAT}}}$
) for propositional formulas is defined as below. The parameter weight of an assignment s is the number of variables mapped to 1 by s.

The classes of the
![]() $\mathbf{W}$
-hierarchy are defined equivalently in terms of these problems.
$\mathbf{W}$
-hierarchy are defined equivalently in terms of these problems.
Proposition 6. (Flum and Grohe Reference Flum and Grohe2006, Thm. 7.1). For every
![]() $t\geq 1$
the following problems are
$t\geq 1$
the following problems are
![]() ${{\mathbf{W}[t]}}$
-complete under fpt-reductions.
${{\mathbf{W}[t]}}$
-complete under fpt-reductions.
-
 $\text{p-}{{\mathrm{WSAT}(\Gamma^+_{t,1},)}}$
if t is even and
$\text{p-}{{\mathrm{WSAT}(\Gamma^+_{t,1},)}}$
if t is even and
 $\text{p-}{{\mathrm{WSAT}(\Gamma^-_{t,1})}}{}$
if t is odd.
$\text{p-}{{\mathrm{WSAT}(\Gamma^-_{t,1})}}{}$
if t is odd. -
 $\text{p-}{{\mathrm{WSAT}(\Gamma_{t,d})}}{}$
for every
$\text{p-}{{\mathrm{WSAT}(\Gamma_{t,d})}}{}$
for every
 $t,d\geq 1$
.
$t,d\geq 1$
.
Fig. 1 draws the complexity landscape with complete problems in parameterized complexity that are relevant.

Figure 1. Landscape of relevant parameterized complexity classes with complete problems. The definition of several of these complete problems is mentioned in the relevant proofs.
Team-based Logics. We assume basic familiarity with predicate logic (Ebbinghaus and Flum Reference Ebbinghaus and Flum1995). We consider first-order vocabularies
![]() $\tau$
that are sets of function symbols and relation symbols with an equality symbol
$\tau$
that are sets of function symbols and relation symbols with an equality symbol
![]() $=$
. Let VAR be a countably infinite set of first-order variables. Terms over
$=$
. Let VAR be a countably infinite set of first-order variables. Terms over
![]() $\tau$
are defined in the usual way, and the set of well-formed formulas of first-order logic (
$\tau$
are defined in the usual way, and the set of well-formed formulas of first-order logic (
![]() ${{\mathcal{FO}}}$
) in negation normal form is defined by the following EBNF:
${{\mathcal{FO}}}$
) in negation normal form is defined by the following EBNF:
where
![]() $t_i$
are terms
$t_i$
are terms
![]() $1\leq i\leq k$
, R is a k-ary relation symbol from
$1\leq i\leq k$
, R is a k-ary relation symbol from
![]() $\sigma$
,
$\sigma$
,
![]() $k\in\mathbb N$
, and
$k\in\mathbb N$
, and
![]() $x\in\mathrm{VAR}$
. If
$x\in\mathrm{VAR}$
. If
![]() $\psi$
is a formula, then we use
$\psi$
is a formula, then we use
![]() $\mathrm{VAR}(\psi)$
for its set of variables, and
$\mathrm{VAR}(\psi)$
for its set of variables, and
![]() ${{\mathrm{Fr}}}(\psi)$
for its set of free variables. We evaluate
${{\mathrm{Fr}}}(\psi)$
for its set of free variables. We evaluate
![]() ${{\mathcal{FO}}}$
-formulas in
${{\mathcal{FO}}}$
-formulas in
![]() $\tau$
-structures, which are pairs of the form
$\tau$
-structures, which are pairs of the form
![]() $\mathcal{A}=(A,\tau^\mathcal{A})$
, where A is the domain of
$\mathcal{A}=(A,\tau^\mathcal{A})$
, where A is the domain of
![]() $\mathcal{A}$
(when clear from the context, we write A instead of
$\mathcal{A}$
(when clear from the context, we write A instead of
![]() $\mathrm{dom}(\mathcal{A})$
), and
$\mathrm{dom}(\mathcal{A})$
), and
![]() $\tau^\mathcal{A}$
interprets the function and relational symbols in the usual way (e.g.,
$\tau^\mathcal{A}$
interprets the function and relational symbols in the usual way (e.g.,
![]() $t^\mathcal{A}\langle s\rangle=s(x)$
if
$t^\mathcal{A}\langle s\rangle=s(x)$
if
![]() $t=x\in\mathrm{VAR}$
). If
$t=x\in\mathrm{VAR}$
). If
![]() $\mathbf t=(t_1,\dots,t_n)$
is a tuple of terms for
$\mathbf t=(t_1,\dots,t_n)$
is a tuple of terms for
![]() $n\in\mathbb N$
, then we write
$n\in\mathbb N$
, then we write
![]() $\mathbf t^\mathcal{A}\langle s\rangle$
for
$\mathbf t^\mathcal{A}\langle s\rangle$
for
![]() $(t_1^\mathcal{A}\langle s\rangle, \dots, t_n^\mathcal{A}\langle s\rangle)$
.
$(t_1^\mathcal{A}\langle s\rangle, \dots, t_n^\mathcal{A}\langle s\rangle)$
.
Dependence logic
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
extends
${{\mathcal{FO}(\mathsf{dep})}}$
extends
![]() ${{\mathcal{FO}}}$
by dependence atoms of the form
${{\mathcal{FO}}}$
by dependence atoms of the form
![]() ${\mathsf{dep}}({\mathbf{t}};{{u}})$
where
${\mathsf{dep}}({\mathbf{t}};{{u}})$
where
![]() $\mathbf t$
and
$\mathbf t$
and
![]() $\mathbf u$
are tuples of terms. Inclusion logic
$\mathbf u$
are tuples of terms. Inclusion logic
![]() ${{\mathcal{FO}(\subseteq)}}$
is obtained by adding to
${{\mathcal{FO}(\subseteq)}}$
is obtained by adding to
![]() ${{\mathcal{FO}}}$
the inclusion atoms of the form
${{\mathcal{FO}}}$
the inclusion atoms of the form
![]() ${\mathbf{t}}\subseteq\mathbf{u}$
for tuples
${\mathbf{t}}\subseteq\mathbf{u}$
for tuples
![]() $\mathbf t$
and
$\mathbf t$
and
![]() $ \mathbf u$
of terms. Finally, independence logic
$ \mathbf u$
of terms. Finally, independence logic
![]() ${{\mathcal{FO}(\bot)}}$
extends
${{\mathcal{FO}(\bot)}}$
extends
![]() ${{\mathcal{FO}}}$
by independence atoms of the form
${{\mathcal{FO}}}$
by independence atoms of the form
![]() ${\mathbf{t}}\bot_{\mathbf{v}}\mathbf{u}$
for tuples
${\mathbf{t}}\bot_{\mathbf{v}}\mathbf{u}$
for tuples
![]() $\mathbf t, \mathbf u$
, and
$\mathbf t, \mathbf u$
, and
![]() $\mathbf v$
of terms. We call expressions of the kind
$\mathbf v$
of terms. We call expressions of the kind
![]() $t_1=t_2, R(\mathbf t),{\mathsf{dep}}({\mathbf{t}};\,{{u}}),{\mathbf{t}}\subseteq\mathbf{u}$
and
$t_1=t_2, R(\mathbf t),{\mathsf{dep}}({\mathbf{t}};\,{{u}}),{\mathbf{t}}\subseteq\mathbf{u}$
and
![]() ${\mathbf{t}}\bot_{\mathbf{v}}\mathbf{u}$
atomic formulas.
${\mathbf{t}}\bot_{\mathbf{v}}\mathbf{u}$
atomic formulas.
The semantics is defined through the concept of a team. Let
![]() $\mathcal{A}$
be a structure and
$\mathcal{A}$
be a structure and
![]() $X\subseteq\mathrm{VAR}$
, then an assignment s is a mapping
$X\subseteq\mathrm{VAR}$
, then an assignment s is a mapping
![]() $s\colon X\rightarrow A$
.
$s\colon X\rightarrow A$
.
Definition 7. Let
![]() $X\subseteq\mathrm{VAR}$
. A team T in
$X\subseteq\mathrm{VAR}$
. A team T in
![]() $\mathcal{A}$
with domain X is a set of assignments
$\mathcal{A}$
with domain X is a set of assignments
![]() $s\colon X\to A$
.
$s\colon X\to A$
.
For a team T with domain
![]() $X\supseteq Y$
define its restriction to Y as
$X\supseteq Y$
define its restriction to Y as
![]() $T{\upharpoonright} Y\:=\{\,s{\upharpoonright} Y \mid s\in T\,\}$
. If
$T{\upharpoonright} Y\:=\{\,s{\upharpoonright} Y \mid s\in T\,\}$
. If
![]() $s\colon X\to A$
is an assignment and
$s\colon X\to A$
is an assignment and
![]() $x\in\mathrm{VAR}$
is a variable, then
$x\in\mathrm{VAR}$
is a variable, then
![]() $s^x_a\colon X\cup\{x\}\to A$
is the assignment that maps x to a and
$s^x_a\colon X\cup\{x\}\to A$
is the assignment that maps x to a and
![]() $y\in X\setminus\{x\}$
to s(y). Let T be a team in
$y\in X\setminus\{x\}$
to s(y). Let T be a team in
![]() $\mathcal{A}$
with domain X. Then any function
$\mathcal{A}$
with domain X. Then any function
![]() $f\colon T\to \mathcal{P}(A)\setminus\{\emptyset\}$
can be used as a supplementing function of T to extend or modify T to the supplemented team
$f\colon T\to \mathcal{P}(A)\setminus\{\emptyset\}$
can be used as a supplementing function of T to extend or modify T to the supplemented team
![]() $T^x_f\:=\{\,s^x_a\mid s\in T,a\in f(s)\,\}$
. For the case
$T^x_f\:=\{\,s^x_a\mid s\in T,a\in f(s)\,\}$
. For the case
![]() $f(s)=A$
is the constant function, we simply write
$f(s)=A$
is the constant function, we simply write
![]() $T^x_\mathcal{A}$
for
$T^x_\mathcal{A}$
for
![]() $T^x_f$
. The semantics of formulas is defined as follows.
$T^x_f$
. The semantics of formulas is defined as follows.
Definition 8. Let
![]() $\tau$
be a vocabulary,
$\tau$
be a vocabulary,
![]() $\mathcal{A}$
be a
$\mathcal{A}$
be a
![]() $\tau$
-structure and T be a team over
$\tau$
-structure and T be a team over
![]() $\mathcal{A}$
with domain
$\mathcal{A}$
with domain
![]() $X\subseteq\mathrm{VAR}$
. Then,
$X\subseteq\mathrm{VAR}$
. Then,
 \begin{alignat*}{3} & \mathcal{A},T\models t_1=t_2 && \;\text{ iff }\; && \forall s\in T: t_1^\mathcal{A}\langle s\rangle=t_2^\mathcal{A}\langle s\rangle,\\ & \mathcal{A},T\models t_1\neq t_2 && \;\text{ iff }\; && \forall s\in T: t_1^\mathcal{A}\langle s\rangle\neq t_2^\mathcal{A}\langle s\rangle,\\ & \mathcal{A},T\models R(t_1,\dots,t_n) && \;\text{ iff }\; && \forall s\in T: (t_1^\mathcal{A}\langle s\rangle,\dots,t_n^\mathcal{A}\langle s\rangle)\in R^{\mathcal{A}},\\ & \mathcal{A},T\models \neg R(t_1,\dots,t_n) && \;\text{ iff }\; && \forall s\in T: (t_1^\mathcal{A}\langle s\rangle,\dots,t_n^\mathcal{A}\langle s\rangle)\not\in R^{\mathcal{A}},\\ & \mathcal{A},T\models {\mathsf{dep}}({\mathbf{t}};{{u}}) && \;\text{ iff }\; && \forall s_1, s_2\in T: \mathbf t^\mathcal{A}\langle s_1\rangle=\mathbf t^\mathcal{A}\langle s_2\rangle \implies \mathbf u^\mathcal{A}\langle s_1\rangle=\mathbf u^\mathcal{A}\langle s_2\rangle ,\\ & \mathcal{A},T\models {\mathbf{t}}\subseteq\mathbf{u} && \;\text{ iff }\; && \forall s_1\in T, \exists s_2\in T: \mathbf t^\mathcal{A}\langle s_1\rangle=\mathbf u^\mathcal{A}\langle s_2\rangle, \\ & \mathcal{A},T\models {\mathbf{t}}\bot_{\mathbf{v}}\mathbf{u} && \;\text{ iff }\; && \forall s_1, s_2\in T: \mathbf v^\mathcal{A}\langle s_1\rangle=\mathbf v^\mathcal{A}\langle s_2\rangle \text{ then } \exists s_3\in T: \\ & && && \mathbf {vt}^\mathcal{A}\langle s_3\rangle=\mathbf {vt}^\mathcal{A}\langle s_1\rangle \text{ and } \mathbf {u}^\mathcal{A}\langle s_3\rangle=\mathbf {u}^\mathcal{A}\langle s_2\rangle,\\ & \mathcal{A},T\models \varphi_0\land \varphi_1 && \;\text{ iff }\; && \mathcal{A},T\models \varphi_0 \text{ and } \mathcal{A},T\models \varphi_1, \\ & \mathcal{A},T\models \varphi_0\lor \varphi_1 && \;\text{ iff }\; && \exists T_0\exists T_1: T_0\cup T_1=T \text{ and } \mathcal{A},T_i\models \varphi_i \, \text{ for }i =0,1,\\ & \mathcal{A},T\models\exists x\varphi && \;\text{ iff }\; && \mathcal{A},T^x_f\models\varphi\text{ for some }f\colon T\to \mathcal{P}(A)\setminus\{\emptyset\},\\ & \mathcal{A},T\models\forall x\varphi && \;\text{ iff }\; && \mathcal{A},T^x_\mathcal{A}\models\varphi.\end{alignat*}
\begin{alignat*}{3} & \mathcal{A},T\models t_1=t_2 && \;\text{ iff }\; && \forall s\in T: t_1^\mathcal{A}\langle s\rangle=t_2^\mathcal{A}\langle s\rangle,\\ & \mathcal{A},T\models t_1\neq t_2 && \;\text{ iff }\; && \forall s\in T: t_1^\mathcal{A}\langle s\rangle\neq t_2^\mathcal{A}\langle s\rangle,\\ & \mathcal{A},T\models R(t_1,\dots,t_n) && \;\text{ iff }\; && \forall s\in T: (t_1^\mathcal{A}\langle s\rangle,\dots,t_n^\mathcal{A}\langle s\rangle)\in R^{\mathcal{A}},\\ & \mathcal{A},T\models \neg R(t_1,\dots,t_n) && \;\text{ iff }\; && \forall s\in T: (t_1^\mathcal{A}\langle s\rangle,\dots,t_n^\mathcal{A}\langle s\rangle)\not\in R^{\mathcal{A}},\\ & \mathcal{A},T\models {\mathsf{dep}}({\mathbf{t}};{{u}}) && \;\text{ iff }\; && \forall s_1, s_2\in T: \mathbf t^\mathcal{A}\langle s_1\rangle=\mathbf t^\mathcal{A}\langle s_2\rangle \implies \mathbf u^\mathcal{A}\langle s_1\rangle=\mathbf u^\mathcal{A}\langle s_2\rangle ,\\ & \mathcal{A},T\models {\mathbf{t}}\subseteq\mathbf{u} && \;\text{ iff }\; && \forall s_1\in T, \exists s_2\in T: \mathbf t^\mathcal{A}\langle s_1\rangle=\mathbf u^\mathcal{A}\langle s_2\rangle, \\ & \mathcal{A},T\models {\mathbf{t}}\bot_{\mathbf{v}}\mathbf{u} && \;\text{ iff }\; && \forall s_1, s_2\in T: \mathbf v^\mathcal{A}\langle s_1\rangle=\mathbf v^\mathcal{A}\langle s_2\rangle \text{ then } \exists s_3\in T: \\ & && && \mathbf {vt}^\mathcal{A}\langle s_3\rangle=\mathbf {vt}^\mathcal{A}\langle s_1\rangle \text{ and } \mathbf {u}^\mathcal{A}\langle s_3\rangle=\mathbf {u}^\mathcal{A}\langle s_2\rangle,\\ & \mathcal{A},T\models \varphi_0\land \varphi_1 && \;\text{ iff }\; && \mathcal{A},T\models \varphi_0 \text{ and } \mathcal{A},T\models \varphi_1, \\ & \mathcal{A},T\models \varphi_0\lor \varphi_1 && \;\text{ iff }\; && \exists T_0\exists T_1: T_0\cup T_1=T \text{ and } \mathcal{A},T_i\models \varphi_i \, \text{ for }i =0,1,\\ & \mathcal{A},T\models\exists x\varphi && \;\text{ iff }\; && \mathcal{A},T^x_f\models\varphi\text{ for some }f\colon T\to \mathcal{P}(A)\setminus\{\emptyset\},\\ & \mathcal{A},T\models\forall x\varphi && \;\text{ iff }\; && \mathcal{A},T^x_\mathcal{A}\models\varphi.\end{alignat*}
For a structure
![]() $\mathcal{A}$
and a team T over X in
$\mathcal{A}$
and a team T over X in
![]() $\mathcal{A}$
, we let
$\mathcal{A}$
, we let
![]() $\mathrm{rel}(T)$
denote the relation defined by T. That is,
$\mathrm{rel}(T)$
denote the relation defined by T. That is,
![]() $\mathrm{rel}(T)\mathrel{\mathop:}= \{\,\mathbf{a}\mid s(\mathbf{x})=\mathbf{a},s\in T \,\}$
. Moreover, we say that a formula
$\mathrm{rel}(T)\mathrel{\mathop:}= \{\,\mathbf{a}\mid s(\mathbf{x})=\mathbf{a},s\in T \,\}$
. Moreover, we say that a formula
![]() $\varphi$
is flat if for any team T over
$\varphi$
is flat if for any team T over
![]() ${{\mathrm{Fr}}}(\varphi)$
we have that
${{\mathrm{Fr}}}(\varphi)$
we have that
![]() $\mathcal{A},T\models \varphi$
if and only if
$\mathcal{A},T\models \varphi$
if and only if
![]() $\mathcal{A},\{s\}\models \varphi$
for every
$\mathcal{A},\{s\}\models \varphi$
for every
![]() $s\in T$
. The
$s\in T$
. The
![]() ${{\mathcal{FO}}}$
-formulas satisfy this flatness property. Notice that, for
${{\mathcal{FO}}}$
-formulas satisfy this flatness property. Notice that, for
![]() ${{\mathcal{FO}}}$
-formulas, by singleton equivalence, team semantics and classical Tarski semantics coincide, i.e.,
${{\mathcal{FO}}}$
-formulas, by singleton equivalence, team semantics and classical Tarski semantics coincide, i.e.,
![]() $\mathcal{A},\{s\}\models \varphi$
if and only if
$\mathcal{A},\{s\}\models \varphi$
if and only if
![]() $\mathcal{A}\models_s \varphi$
. Furthermore, note that
$\mathcal{A}\models_s \varphi$
. Furthermore, note that
![]() $\mathcal{A},T\models \varphi$
for all
$\mathcal{A},T\models \varphi$
for all
![]() $\varphi$
when
$\varphi$
when
![]() $T=\emptyset$
(this is also called the empty team property). Finally,
$T=\emptyset$
(this is also called the empty team property). Finally,
![]() $\mathcal{C}$
-formulas for every
$\mathcal{C}$
-formulas for every
![]() $\mathcal{C}\in \{{{\mathcal{FO}(\mathsf{dep})}},{{\mathcal{FO}(\subseteq)}},{{\mathcal{FO}(\bot)}}\}$
are local, that is, for a team T in
$\mathcal{C}\in \{{{\mathcal{FO}(\mathsf{dep})}},{{\mathcal{FO}(\subseteq)}},{{\mathcal{FO}(\bot)}}\}$
are local, that is, for a team T in
![]() $\mathcal{A}$
over domain X and a
$\mathcal{A}$
over domain X and a
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula
${{\mathcal{FO}(\mathsf{dep})}}$
-formula
![]() $\varphi$
, we have that
$\varphi$
, we have that
![]() $\mathcal{A},T\models\varphi$
if and only if
$\mathcal{A},T\models\varphi$
if and only if
![]() $\mathcal{A},T{\upharpoonright}{{{\mathrm{Fr}}}(\varphi)}\models\varphi$
.
$\mathcal{A},T{\upharpoonright}{{{\mathrm{Fr}}}(\varphi)}\models\varphi$
.
We now extend the formulas classes (
![]() ${{\mathrm{\Sigma}_{t}}}$
and
${{\mathrm{\Sigma}_{t}}}$
and
![]() ${{\mathrm{\Pi}_{t}}}$
) to the logics under consideration. To this end,
${{\mathrm{\Pi}_{t}}}$
) to the logics under consideration. To this end,
![]() ${{{{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Pi}_{t}}}}}\subseteq{{\mathcal{FO}(\mathsf{dep})}}$
(resp.,
${{{{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Pi}_{t}}}}}\subseteq{{\mathcal{FO}(\mathsf{dep})}}$
(resp.,
![]() ${{{{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Sigma}_{t}}}}}$
) denotes the collection of formulas
${{{{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Sigma}_{t}}}}}$
) denotes the collection of formulas
![]() $\varphi$
of the form
$\varphi$
of the form
![]() $\varphi\mathrel{\mathop:}= Q_1x_1Q_2x_2\dots Q_tx_t\psi$
such that
$\varphi\mathrel{\mathop:}= Q_1x_1Q_2x_2\dots Q_tx_t\psi$
such that
![]() $\psi$
is a quantifier free
$\psi$
is a quantifier free
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula,
${{\mathcal{FO}(\mathsf{dep})}}$
-formula,
![]() $Q_i\in \{\forall,\exists\}$
and
$Q_i\in \{\forall,\exists\}$
and
![]() $Q_1=\forall$
(
$Q_1=\forall$
(
![]() $Q_1=\exists$
). In other words,
$Q_1=\exists$
). In other words,
![]() $\varphi$
is a
$\varphi$
is a
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula that starts with a
${{\mathcal{FO}(\mathsf{dep})}}$
-formula that starts with a
![]() $\forall$
-quantifier (resp.,
$\forall$
-quantifier (resp.,
![]() $\exists$
) and has t-alternations of quantifiers. The classes
$\exists$
) and has t-alternations of quantifiers. The classes
![]() ${{{{\mathcal{FO}(\subseteq)}}\text-{{\mathrm{\Pi}_{t}}}}}\subseteq{{\mathcal{FO}(\subseteq)}}$
(resp.,
${{{{\mathcal{FO}(\subseteq)}}\text-{{\mathrm{\Pi}_{t}}}}}\subseteq{{\mathcal{FO}(\subseteq)}}$
(resp.,
![]() ${{{{\mathcal{FO}(\subseteq)}}\text-{{\mathrm{\Sigma}_{t}}}}}$
) for
${{{{\mathcal{FO}(\subseteq)}}\text-{{\mathrm{\Sigma}_{t}}}}}$
) for
![]() ${{\mathcal{FO}(\subseteq)}}$
and
${{\mathcal{FO}(\subseteq)}}$
and
![]() ${{{{\mathcal{FO}(\bot)}}\text-{{\mathrm{\Pi}_{t}}}}}\subseteq{{\mathcal{FO}(\mathsf{dep})}}$
(resp.,
${{{{\mathcal{FO}(\bot)}}\text-{{\mathrm{\Pi}_{t}}}}}\subseteq{{\mathcal{FO}(\mathsf{dep})}}$
(resp.,
![]() ${{{{\mathcal{FO}(\bot)}}\text-{{\mathrm{\Sigma}_{t}}}}}$
) for
${{{{\mathcal{FO}(\bot)}}\text-{{\mathrm{\Sigma}_{t}}}}}$
) for
![]() ${{\mathcal{FO}(\bot)}}$
are similarly defined.
${{\mathcal{FO}(\bot)}}$
are similarly defined.
Weighted Team Definability. Now we introduce a novel version of the weighted definability problem for formulas in team-based logics. Let
![]() $\mathcal{C}\in \{{{\mathcal{FO}(\mathsf{dep})}},{{\mathcal{FO}(\subseteq)}},{{\mathcal{FO}(\bot)}}\}$
,
$\mathcal{C}\in \{{{\mathcal{FO}(\mathsf{dep})}},{{\mathcal{FO}(\subseteq)}},{{\mathcal{FO}(\bot)}}\}$
,
![]() $\varphi$
be a fixed
$\varphi$
be a fixed
![]() $\mathcal{C}$
-formula over free variables
$\mathcal{C}$
-formula over free variables
![]() ${{\mathrm{Fr}}}(\varphi)$
and
${{\mathrm{Fr}}}(\varphi)$
and
![]() $k\in \mathbb N$
. Then given a structure
$k\in \mathbb N$
. Then given a structure
![]() $\mathcal{A}$
, the weighted-team definable problem
$\mathcal{A}$
, the weighted-team definable problem
![]() $\mathrm{WT}_\varphi$
asks if there is a team of size k for
$\mathrm{WT}_\varphi$
asks if there is a team of size k for
![]() $\varphi$
over
$\varphi$
over
![]() ${{\mathrm{Fr}}}(\varphi)$
in
${{\mathrm{Fr}}}(\varphi)$
in
![]() $\mathcal{A}$
.
$\mathcal{A}$
.

Then the analogous parameterized version of
![]() $\mathrm{WT}_\varphi$
is defined as follows.
$\mathrm{WT}_\varphi$
is defined as follows.

Note that the problem
![]() $\mathrm{WT}_\varphi$
references the set of free variables
$\mathrm{WT}_\varphi$
references the set of free variables
![]() ${{\mathrm{Fr}}}(\varphi)$
of the formula
${{\mathrm{Fr}}}(\varphi)$
of the formula
![]() $\varphi$
. As a consequence, our parameterization is trivial for sentences since there are only two teams
$\varphi$
. As a consequence, our parameterization is trivial for sentences since there are only two teams
![]() $\emptyset$
and
$\emptyset$
and
![]() $\{\emptyset\}$
with the empty team domain. As before, for a set
$\{\emptyset\}$
with the empty team domain. As before, for a set
![]() ${{\mathrm{\Theta}}}\subseteq \mathcal{C}$
of formulas, we denote by
${{\mathrm{\Theta}}}\subseteq \mathcal{C}$
of formulas, we denote by
![]() $\mathrm{WT}\text-{{\mathrm{\Theta}}}$
the class of problems
$\mathrm{WT}\text-{{\mathrm{\Theta}}}$
the class of problems
![]() $\mathrm{WT}_\varphi$
such that
$\mathrm{WT}_\varphi$
such that
![]() $\varphi\in {{\mathrm{\Theta}}}$
.
$\varphi\in {{\mathrm{\Theta}}}$
.
3. Complexity Results for Weighted Team Definability
3.1 First-order formulas
We begin our study of the complexity for
![]() $\text{p-} \mathrm{WT}_\varphi$
in the case
$\text{p-} \mathrm{WT}_\varphi$
in the case
![]() $\varphi $
is a pure
$\varphi $
is a pure
![]() ${{\mathcal{FO}}}$
-formula under team semantics. Notice that the consequence of disallowing free relation variables in
${{\mathcal{FO}}}$
-formula under team semantics. Notice that the consequence of disallowing free relation variables in
![]() $\varphi$
is that
$\varphi$
is that
![]() $\text{p-}\mathrm{WT}_\varphi$
is different than the weighted Fagin definability
$\text{p-}\mathrm{WT}_\varphi$
is different than the weighted Fagin definability
![]() $\text{p-}\mathrm{WD}_\varphi$
. The following theorem establishes that the two problems are also different from the classical complexity theoretic point of view. Here, we assume basic familiarity about the circuit complexity classes
$\text{p-}\mathrm{WD}_\varphi$
. The following theorem establishes that the two problems are also different from the classical complexity theoretic point of view. Here, we assume basic familiarity about the circuit complexity classes
![]() $\mathrm{TC}^0$
and
$\mathrm{TC}^0$
and
![]() $\mathrm{AC}^0$
(for an introduction into this area, see the textbook of Vollmer Reference Vollmer1999).
$\mathrm{AC}^0$
(for an introduction into this area, see the textbook of Vollmer Reference Vollmer1999).
Theorem 9. For any
![]() ${{\mathcal{FO}}}$
-formula
${{\mathcal{FO}}}$
-formula
![]() $\varphi$
the problem
$\varphi$
the problem
![]() $\mathrm{WT}_\varphi$
is in DLOGTIME-uniform
$\mathrm{WT}_\varphi$
is in DLOGTIME-uniform
![]() $\mathrm{TC}^0$
.
$\mathrm{TC}^0$
.
Proof. The proof uses the flatness property of
![]() ${{\mathcal{FO}}}$
-formulas under team semantics:
${{\mathcal{FO}}}$
-formulas under team semantics:
It is well known that
![]() $\mathcal{A}\models_s \varphi$
can be decided by
$\mathcal{A}\models_s \varphi$
can be decided by
![]() $\mathrm{AC}^0$
-circuits, whence the original question reduces to counting the number t of satisfying assignments of
$\mathrm{AC}^0$
-circuits, whence the original question reduces to counting the number t of satisfying assignments of
![]() $\varphi$
and checking whether
$\varphi$
and checking whether
![]() $t\ge k$
. This can be easily simulated by DLOGTIME-uniform
$t\ge k$
. This can be easily simulated by DLOGTIME-uniform
![]() $\mathrm{TC}^0$
circuits as we can hardcode all possible assignments into the circuit. Here, notice that
$\mathrm{TC}^0$
circuits as we can hardcode all possible assignments into the circuit. Here, notice that
![]() $\varphi$
is fixed and thereby the number of free variables are fixed to some constant
$\varphi$
is fixed and thereby the number of free variables are fixed to some constant
![]() $c\in\mathbb N$
. Then, the input is the structure
$c\in\mathbb N$
. Then, the input is the structure
![]() $\mathcal A$
of size n yielding
$\mathcal A$
of size n yielding
![]() $O(n^c)$
many assignments.
$O(n^c)$
many assignments.
3.2 Inclusion logic
In this section, we relate the
![]() ${\mathbf{W}}$
-hierarchy and
${\mathbf{W}}$
-hierarchy and
![]() ${{\mathbf{W}[{{\mathbf{P}}}]}}$
to weighted team definability for inclusion logic formulas. First, observe that if
${{\mathbf{W}[{{\mathbf{P}}}]}}$
to weighted team definability for inclusion logic formulas. First, observe that if
![]() $\varphi$
is an
$\varphi$
is an
![]() ${{\mathcal{FO}(\subseteq)}}$
-sentence, then the problem
${{\mathcal{FO}(\subseteq)}}$
-sentence, then the problem
![]() $\text{p-} \mathrm{WT}_\varphi$
is in
$\text{p-} \mathrm{WT}_\varphi$
is in
![]() ${{\mathbf{FPT}}}$
. This is due to the reason that the data complexity of fixed
${{\mathbf{FPT}}}$
. This is due to the reason that the data complexity of fixed
![]() ${{\mathcal{FO}(\subseteq)}}$
-sentences is in
${{\mathcal{FO}(\subseteq)}}$
-sentences is in
![]() ${{\mathbf{P}}}$
(Galliani and Hella Reference Galliani, Hella and Della Rocca2013).
${{\mathbf{P}}}$
(Galliani and Hella Reference Galliani, Hella and Della Rocca2013).
Theorem 10. Let
![]() $\varphi$
be an
$\varphi$
be an
![]() ${{\mathcal{FO}(\subseteq)}}$
-sentence, then
${{\mathcal{FO}(\subseteq)}}$
-sentence, then
![]() $\text{p-}\mathrm{WT}_{\varphi}$
is in
$\text{p-}\mathrm{WT}_{\varphi}$
is in
![]() ${{\mathbf{FPT}}}$
.
${{\mathbf{FPT}}}$
.
Proof. Recall that an
![]() ${{\mathcal{FO}(\subseteq)}}$
-sentence
${{\mathcal{FO}(\subseteq)}}$
-sentence
![]() $\varphi$
has a satisfying team T in
$\varphi$
has a satisfying team T in
![]() $\mathcal{A}$
if and only if
$\mathcal{A}$
if and only if
![]() $\mathcal{A},\{\emptyset\}\models \varphi$
due to the locality property. Then
$\mathcal{A},\{\emptyset\}\models \varphi$
due to the locality property. Then
![]() $\varphi$
is true in
$\varphi$
is true in
![]() $\mathcal{A}$
if and only if there is a team T such that
$\mathcal{A}$
if and only if there is a team T such that
![]() $|T|=1$
and
$|T|=1$
and
![]() $\mathcal{A},T\models \varphi$
.
$\mathcal{A},T\models \varphi$
.
Now we prove, that
![]() $\text{p-}\mathrm{WT}_\varphi$
can already be
$\text{p-}\mathrm{WT}_\varphi$
can already be
![]() ${{\mathbf{W}[1]}}$
-hard when
${{\mathbf{W}[1]}}$
-hard when
![]() $\varphi$
is a quantifier-free
$\varphi$
is a quantifier-free
![]() ${{\mathcal{FO}}}(\subseteq)$
-formula with free variables.
${{\mathcal{FO}}}(\subseteq)$
-formula with free variables.
Theorem 11. There is a quantifier-free
![]() ${{\mathcal{FO}}}(\subseteq)$
-formula
${{\mathcal{FO}}}(\subseteq)$
-formula
![]() $\varphi$
such that the problem
$\varphi$
such that the problem
![]() $\text{p-}\mathrm{WT}_\varphi$
is
$\text{p-}\mathrm{WT}_\varphi$
is
![]() ${{\mathbf{W}[1]}}$
-hard and in
${{\mathbf{W}[1]}}$
-hard and in
![]() ${{\mathbf{W}[2]}}$
.
${{\mathbf{W}[2]}}$
.
Proof. We present a reduction from the
![]() ${{\mathbf{W}[1]}}$
-complete problem
${{\mathbf{W}[1]}}$
-complete problem ![]() to
to
![]() $\text{p-}\mathrm{WT}_\varphi$
such that
$\text{p-}\mathrm{WT}_\varphi$
such that
![]() $\varphi$
is a quantifier free
$\varphi$
is a quantifier free
![]() ${{\mathcal{FO}(\subseteq)}}$
-formula. Let
${{\mathcal{FO}(\subseteq)}}$
-formula. Let
![]() $G\mathrel{\mathop:}= (V,E)$
be a graph and
$G\mathrel{\mathop:}= (V,E)$
be a graph and
![]() $k\in \mathbb N$
. Then, we let
$k\in \mathbb N$
. Then, we let
![]() $\varphi\:= E(x,y)\wedge x\neq y\wedge y\subseteq x \wedge x\subseteq y$
. We claim that G has a clique of size k if and only if
$\varphi\:= E(x,y)\wedge x\neq y\wedge y\subseteq x \wedge x\subseteq y$
. We claim that G has a clique of size k if and only if
![]() $G,T\models \varphi$
for a team T of size
$G,T\models \varphi$
for a team T of size
![]() $(k^2-k)$
. It is easy to check that the existence of a k-clique is equivalent to
$(k^2-k)$
. It is easy to check that the existence of a k-clique is equivalent to
![]() $\varphi $
having a satisfying team of cardinality
$\varphi $
having a satisfying team of cardinality
![]() $k(k-1)$
. Clearly, a clique of size k contains
$k(k-1)$
. Clearly, a clique of size k contains
![]() $k(k-1)$
-many edges. Then the variables x and y take same values under each assignment in the resulting team which form a clique.
$k(k-1)$
-many edges. Then the variables x and y take same values under each assignment in the resulting team which form a clique.
For containment in
![]() ${{\mathbf{W}[2]}}$
, it suffices to note that the formula
${{\mathbf{W}[2]}}$
, it suffices to note that the formula
![]() $\varphi$
can be expressed as an
$\varphi$
can be expressed as an
![]() ${{\mathcal{FO}}}$
-sentence
${{\mathcal{FO}}}$
-sentence
![]() $\psi(S)$
with a
$\psi(S)$
with a
![]() $\forall\exists$
-quantifier prefix where the auxiliary binary predicate S encodes the team T. This gives an
$\forall\exists$
-quantifier prefix where the auxiliary binary predicate S encodes the team T. This gives an
![]() ${{\mathbf{FPT}}}$
-reduction between
${{\mathbf{FPT}}}$
-reduction between
![]() $\text{p-}\mathrm{WT}_\varphi$
and
$\text{p-}\mathrm{WT}_\varphi$
and
![]() $\text{p-}\mathrm{WD}_\psi$
. The result follows since
$\text{p-}\mathrm{WD}_\psi$
. The result follows since
![]() ${{\mathbf{W}[2]}}\mathrel{\mathop:}=[\text{p-}\mathrm{WD}\text-{{\mathrm{\Pi}_{2}}}]$
.
${{\mathbf{W}[2]}}\mathrel{\mathop:}=[\text{p-}\mathrm{WD}\text-{{\mathrm{\Pi}_{2}}}]$
.
This result can be strengthened to more general formulas as witnessed by the following corollary.
Corollary 12. For any quantifier-free
![]() ${{\mathcal{FO}}}(\subseteq)$
-formula
${{\mathcal{FO}}}(\subseteq)$
-formula
![]() $\varphi$
without
$\varphi$
without
![]() $\lor$
, the problem
$\lor$
, the problem
![]() $\text{p-}\mathrm{WT}_\varphi$
is in
$\text{p-}\mathrm{WT}_\varphi$
is in
![]() ${{\mathbf{W}[2]}}$
.
${{\mathbf{W}[2]}}$
.
Proof. For containment in
![]() ${{\mathbf{W}[2]}}$
, it suffices to note that the any quantifier-free formula without disjunction can be expressed as an
${{\mathbf{W}[2]}}$
, it suffices to note that the any quantifier-free formula without disjunction can be expressed as an
![]() ${{\mathcal{FO}}}$
-sentence
${{\mathcal{FO}}}$
-sentence
![]() $\psi(S)$
with a
$\psi(S)$
with a
![]() $\forall\exists$
-quantifier prefix where the auxiliary binary predicate S encodes the team T.
$\forall\exists$
-quantifier prefix where the auxiliary binary predicate S encodes the team T.
Theorem 13. There is an
![]() ${{\mathcal{FO}}}(\subseteq)$
-formula
${{\mathcal{FO}}}(\subseteq)$
-formula
![]() $\varphi$
with
$\varphi$
with
![]() $\forall\exists$
-quantifier prefix for which the problem
$\forall\exists$
-quantifier prefix for which the problem
![]() $\text{p-}\mathrm{WT}_\varphi$
is
$\text{p-}\mathrm{WT}_\varphi$
is
![]() ${{\mathbf{W}[2]}}$
-complete.
${{\mathbf{W}[2]}}$
-complete.
Proof. We present a reduction from the
![]() ${{\mathbf{W}[2]}}$
-complete problem
${{\mathbf{W}[2]}}$
-complete problem ![]() to
to
![]() $\text{p-}\mathrm{WT}_\varphi$
such that
$\text{p-}\mathrm{WT}_\varphi$
such that
![]() $\varphi$
is a
$\varphi$
is a
![]() ${{\mathcal{FO}(\subseteq)}}$
-formula with
${{\mathcal{FO}(\subseteq)}}$
-formula with
![]() $\forall\exists$
-quantifier prefix. Let
$\forall\exists$
-quantifier prefix. Let
![]() $G\mathrel{\mathop:}= (V,E)$
be a graph and
$G\mathrel{\mathop:}= (V,E)$
be a graph and
![]() $k\in \mathbb N$
. Then we let,
$k\in \mathbb N$
. Then we let,
![]() $\varphi\mathrel{\mathop:}= \forall x \exists y (y\subseteq z \wedge ( E(x,y)\vee x=y))$
. It is straightforward to check that G has a dominating set of size k if and only if
$\varphi\mathrel{\mathop:}= \forall x \exists y (y\subseteq z \wedge ( E(x,y)\vee x=y))$
. It is straightforward to check that G has a dominating set of size k if and only if
![]() $G,T\models \varphi$
for a team T with domain
$G,T\models \varphi$
for a team T with domain
![]() $\{z\}$
of size k.
$\{z\}$
of size k.
For
![]() ${{\mathbf{W}[2]}}$
-membership, notice that for all graphs G and teams T:
${{\mathbf{W}[2]}}$
-membership, notice that for all graphs G and teams T:
where
![]() $\varphi_d(X)$
is the first-order sentence encoding the problem
$\varphi_d(X)$
is the first-order sentence encoding the problem ![]() (see Example 2). A formal proof for the above equivalence is similar to the one given in Theorem 19.
(see Example 2). A formal proof for the above equivalence is similar to the one given in Theorem 19.
The next lemma sets the stage for generalizing the two previous theorems to arbitrary levels of the
![]() ${\mathbf{W}}$
-hierarchy. To formulate the result, we assume an encoding of a formula
${\mathbf{W}}$
-hierarchy. To formulate the result, we assume an encoding of a formula
![]() $\psi \in \Gamma^{+}_{t,d}$
(and a truth assignment) by its syntax circuit defined as follows.
$\psi \in \Gamma^{+}_{t,d}$
(and a truth assignment) by its syntax circuit defined as follows.
Definition 14. Let
![]() $\psi \in \Gamma^{+}_{t,d}$
be a propositional formula. We define the syntax circuit for
$\psi \in \Gamma^{+}_{t,d}$
be a propositional formula. We define the syntax circuit for
![]() $\psi$
by
$\psi$
by
![]() $A_{\psi}=(A,E,I,o)$
, where A is the set of subformulas of
$A_{\psi}=(A,E,I,o)$
, where A is the set of subformulas of
![]() $\psi$
, E is the immediate subformula relation,
$\psi$
, E is the immediate subformula relation,
![]() $I\subseteq A$
are the variables of
$I\subseteq A$
are the variables of
![]() $\psi$
, and o is a constant symbol interpreted by
$\psi$
, and o is a constant symbol interpreted by
![]() $\psi$
. Moreover, we use a free relation variable
$\psi$
. Moreover, we use a free relation variable
![]() $S\subseteq I$
to represent a truth assignment for the variables of
$S\subseteq I$
to represent a truth assignment for the variables of
![]() $\psi$
.
$\psi$
.
Note that our encoding of
![]() $\psi$
works for any
$\psi$
works for any
![]() $t\in \mathbb N$
but for the definability result below t has to be fixed.
$t\in \mathbb N$
but for the definability result below t has to be fixed.
Lemma 15. Let
![]() $t\in \mathbb{N}$
. Then there exists a fixed formula
$t\in \mathbb{N}$
. Then there exists a fixed formula
![]() $\varphi_t\in {{\mathcal{FO}}}(\subseteq)$
with one free variable z such that for all
$\varphi_t\in {{\mathcal{FO}}}(\subseteq)$
with one free variable z such that for all
![]() $\psi \in \Gamma^{+}_{t,d}$
and
$\psi \in \Gamma^{+}_{t,d}$
and
![]() $k\ge 1$
:
$k\ge 1$
:
![]() $\psi$
has a satisfying assignment of weight k if and only if
$\psi$
has a satisfying assignment of weight k if and only if
![]() $A_{\psi},T\models \varphi_t$
, for some team T of cardinality k.
$A_{\psi},T\models \varphi_t$
, for some team T of cardinality k.
Proof. Without loss of generality, we assume
![]() $d=1$
. For higher d-values, the presented proof easily generalizes via a conjunction/disjunction of arity d. By the results of Galliani and Hella (Reference Galliani, Hella and Della Rocca2013), it suffices to show that the required formula can be expressed by a first-order sentence
$d=1$
. For higher d-values, the presented proof easily generalizes via a conjunction/disjunction of arity d. By the results of Galliani and Hella (Reference Galliani, Hella and Della Rocca2013), it suffices to show that the required formula can be expressed by a first-order sentence
![]() $\theta(S)$
in which the relation symbol S occurs only positively. Then the existence of
$\theta(S)$
in which the relation symbol S occurs only positively. Then the existence of
![]() $\varphi_t(z)$
satisfying
$\varphi_t(z)$
satisfying
for all nonempty T and
![]() $\mathrm{rel}(T)=S$
follows. Note that
$\mathrm{rel}(T)=S$
follows. Note that
![]() $\theta(S)$
is not true under the assignment setting all the variables to false, but on the other hand
$\theta(S)$
is not true under the assignment setting all the variables to false, but on the other hand
![]() $\varphi_t$
is always satisfied for
$\varphi_t$
is always satisfied for
![]() $T=\emptyset$
by the empty team property. It is easy to check that, for an even t,
$T=\emptyset$
by the empty team property. It is easy to check that, for an even t,
![]() $\theta(S)$
can be expressed as follows:
$\theta(S)$
can be expressed as follows:
In the case t is odd the conjunction after
![]() $E(x_{t-1},x_t)$
has to be replaced by an implication. The relation symbol S has only one occurrence in the formula and it is positive. Now by Proposition 20 of Galliani and Hella (Reference Galliani, Hella and Della Rocca2013), there exists an
$E(x_{t-1},x_t)$
has to be replaced by an implication. The relation symbol S has only one occurrence in the formula and it is positive. Now by Proposition 20 of Galliani and Hella (Reference Galliani, Hella and Della Rocca2013), there exists an
![]() ${{\mathcal{FO}(\subseteq)}}$
-formula
${{\mathcal{FO}(\subseteq)}}$
-formula
![]() $\varphi_t$
such (1) holds for the sentence
$\varphi_t$
such (1) holds for the sentence
![]() $\forall \vec{x}(S(\vec{x})\rightarrow \theta(S))$
for all
$\forall \vec{x}(S(\vec{x})\rightarrow \theta(S))$
for all
![]() $\mathcal{A}$
and all T. It is easy to see that
$\mathcal{A}$
and all T. It is easy to see that
![]() $\theta(S)$
is equivalent with
$\theta(S)$
is equivalent with
![]() $\forall \vec{x}(S(\vec{x})\rightarrow \theta(S))$
modulo the cases when
$\forall \vec{x}(S(\vec{x})\rightarrow \theta(S))$
modulo the cases when
![]() $S=\emptyset$
. In fact, it is straightforward to show that
$S=\emptyset$
. In fact, it is straightforward to show that
![]() $\varphi_t$
can be obtained from
$\varphi_t$
can be obtained from
![]() $\theta(S)$
simply by replacing
$\theta(S)$
simply by replacing
![]() $S(x_t)$
by the inclusion atom
$S(x_t)$
by the inclusion atom
![]() $x_t\subseteq z$
. The proof then is analogous to the proof of Theorem 19.
$x_t\subseteq z$
. The proof then is analogous to the proof of Theorem 19.
Notice further that the translation of the formula
![]() $\theta$
to an
$\theta$
to an
![]() ${{\mathcal{FO}(\subseteq)}}$
-formula only introduces inclusion atoms and, in particular, does not require any further quantification. Therefore, the following corollary follows immediately from the proof in Lemma 15.
${{\mathcal{FO}(\subseteq)}}$
-formula only introduces inclusion atoms and, in particular, does not require any further quantification. Therefore, the following corollary follows immediately from the proof in Lemma 15.
Corollary 16. Let
![]() $t\geq 2$
be even. Then there is an
$t\geq 2$
be even. Then there is an
![]() ${{\mathcal{FO}}}(\subseteq)\text-{{\mathrm{\Pi}_{t}}}$
-formula
${{\mathcal{FO}}}(\subseteq)\text-{{\mathrm{\Pi}_{t}}}$
-formula
![]() ${\varphi_t}$
for which the problem
${\varphi_t}$
for which the problem
![]() $\text{p-}\mathrm{WT}_{\varphi_t}$
is
$\text{p-}\mathrm{WT}_{\varphi_t}$
is
![]() ${{\mathbf{W}[t]}}$
-complete. Moreover,
${{\mathbf{W}[t]}}$
-complete. Moreover,
![]() ${{\mathbf{W}[t]}} \subseteq [\text{p-}\mathrm{WT}\text-{{{{\mathcal{FO}(\subseteq)}}\text-{{\mathrm{\Pi}_{t}}}}}]^{{{\mathbf{FPT}}}}$
for all even
${{\mathbf{W}[t]}} \subseteq [\text{p-}\mathrm{WT}\text-{{{{\mathcal{FO}(\subseteq)}}\text-{{\mathrm{\Pi}_{t}}}}}]^{{{\mathbf{FPT}}}}$
for all even
![]() $t\geq 1$
and
$t\geq 1$
and
![]() $\bigcup_{t\ge1}{{\mathbf{W}[t]}} \subseteq [\text{p-}\mathrm{WT}\text-{{\mathcal{FO}(\subseteq)}}]^{{{\mathbf{FPT}}}}$
.
$\bigcup_{t\ge1}{{\mathbf{W}[t]}} \subseteq [\text{p-}\mathrm{WT}\text-{{\mathcal{FO}(\subseteq)}}]^{{{\mathbf{FPT}}}}$
.
Proof. For the
![]() ${{\mathbf{W}[t]}}$
-membership of
${{\mathbf{W}[t]}}$
-membership of
![]() $\text{p-}\mathrm{WT}_{\varphi_t}$
, notice that the translation between
$\text{p-}\mathrm{WT}_{\varphi_t}$
, notice that the translation between
![]() $\theta$
and the
$\theta$
and the
![]() ${{\mathcal{FO}(\subseteq)}}$
-formula
${{\mathcal{FO}(\subseteq)}}$
-formula
![]() $\varphi_t$
in the proof of Lemma 15 preserves a one-to-one correspondence between the solutions S for
$\varphi_t$
in the proof of Lemma 15 preserves a one-to-one correspondence between the solutions S for
![]() $\theta$
and satisfying teams T for
$\theta$
and satisfying teams T for
![]() $\varphi_t$
. In other words,
$\varphi_t$
. In other words,
![]() $\theta$
has a solution of size k if and only if
$\theta$
has a solution of size k if and only if
![]() $\varphi_t$
has a satisfying team of size k. This yields
$\varphi_t$
has a satisfying team of size k. This yields
![]() ${{\mathbf{W}[t]}}$
-membership since
${{\mathbf{W}[t]}}$
-membership since
![]() $\theta\in {{\mathrm{\Pi}_{t}}}$
for each
$\theta\in {{\mathrm{\Pi}_{t}}}$
for each
![]() $t\geq 1$
(see Def. 5). The
$t\geq 1$
(see Def. 5). The
![]() ${{\mathbf{W}[t]}}$
-hardness and the containment
${{\mathbf{W}[t]}}$
-hardness and the containment
![]() ${{\mathbf{W}[t]}} \subseteq [\text{p-}\mathrm{WT}\text-{{{{\mathcal{FO}(\subseteq)}}\text-{{\mathrm{\Pi}_{t}}}}}]^{{{\mathbf{FPT}}}}$
for all even
${{\mathbf{W}[t]}} \subseteq [\text{p-}\mathrm{WT}\text-{{{{\mathcal{FO}(\subseteq)}}\text-{{\mathrm{\Pi}_{t}}}}}]^{{{\mathbf{FPT}}}}$
for all even
![]() $t\geq 1$
follows from Proposition 6.
$t\geq 1$
follows from Proposition 6.
We conclude this section by presenting the upper bounds for
![]() $\mathrm{WT}_\varphi$
when
$\mathrm{WT}_\varphi$
when
![]() $\varphi$
is an arbitrary
$\varphi$
is an arbitrary
![]() $ {{\mathcal{FO}}}(\subseteq)$
-formula.
$ {{\mathcal{FO}}}(\subseteq)$
-formula.
Theorem 17.
![]() $[\text{p-}\mathrm{WT}\text-{{\mathcal{FO}}}(\subseteq)]^{{{\mathbf{FPT}}}}\subseteq {{\mathbf{W}[{{\mathbf{P}}}]}}$
.
$[\text{p-}\mathrm{WT}\text-{{\mathcal{FO}}}(\subseteq)]^{{{\mathbf{FPT}}}}\subseteq {{\mathbf{W}[{{\mathbf{P}}}]}}$
.
Proof. We prove this via the machine characterization of the class
![]() ${{\mathbf{W}[{{\mathbf{P}}}]}}$
, analogous to the proof for
${{\mathbf{W}[{{\mathbf{P}}}]}}$
, analogous to the proof for
![]() ${{\mathcal{FO}}}$
-formulas (Flum and Grohe Reference Flum and Grohe2006, Prop. 5.3). Let
${{\mathcal{FO}}}$
-formulas (Flum and Grohe Reference Flum and Grohe2006, Prop. 5.3). Let
![]() $\varphi$
be a
$\varphi$
be a
![]() ${{\mathcal{FO}}}(\subseteq)$
-formula with s free variables. An algorithm for the problem
${{\mathcal{FO}}}(\subseteq)$
-formula with s free variables. An algorithm for the problem
![]() $\text{p-}\mathrm{WT}_\varphi$
proceeds as follows: Given a structure
$\text{p-}\mathrm{WT}_\varphi$
proceeds as follows: Given a structure
![]() $\mathcal{A}$
and a k, nondeterministically guess k times an assignment (i.e., an s-tuple of elements of
$\mathcal{A}$
and a k, nondeterministically guess k times an assignment (i.e., an s-tuple of elements of
![]() $\mathcal{A}$
), then deterministically verify that the team T has cardinality k and
$\mathcal{A}$
), then deterministically verify that the team T has cardinality k and
![]() $\mathcal{A},T\models \varphi$
. Guessing T requires
$\mathcal{A},T\models \varphi$
. Guessing T requires
![]() $s \cdot k\cdot \log |A|$
nondeterministic bits, and the verification that
$s \cdot k\cdot \log |A|$
nondeterministic bits, and the verification that
![]() $\mathcal{A},T\models \varphi$
can be done in deterministic polynomial time in
$\mathcal{A},T\models \varphi$
can be done in deterministic polynomial time in
![]() $|A|$
(Galliani and Hella Reference Galliani, Hella and Della Rocca2013). Thus,
$|A|$
(Galliani and Hella Reference Galliani, Hella and Della Rocca2013). Thus,
![]() $\text{p-}\mathrm{WT}_\varphi$
is in
$\text{p-}\mathrm{WT}_\varphi$
is in
![]() ${{\mathbf{W}[{{\mathbf{P}}}]}}$
because the formula
${{\mathbf{W}[{{\mathbf{P}}}]}}$
because the formula
![]() $\varphi$
is fixed and s is a constant. Moreover, the containment
$\varphi$
is fixed and s is a constant. Moreover, the containment
![]() $[\text{p-}\mathrm{WT}\text-{{\mathcal{FO}}}(\subseteq)]^{{{\mathbf{FPT}}}}\subseteq {{\mathbf{W}[{{\mathbf{P}}}]}}$
holds since
$[\text{p-}\mathrm{WT}\text-{{\mathcal{FO}}}(\subseteq)]^{{{\mathbf{FPT}}}}\subseteq {{\mathbf{W}[{{\mathbf{P}}}]}}$
holds since
![]() $\text{p-}\mathrm{WT}_\varphi\in {{\mathbf{W}[{{\mathbf{P}}}]}}$
for an arbitrary but fixed
$\text{p-}\mathrm{WT}_\varphi\in {{\mathbf{W}[{{\mathbf{P}}}]}}$
for an arbitrary but fixed
![]() ${{\mathcal{FO}(\subseteq)}}$
-formula
${{\mathcal{FO}(\subseteq)}}$
-formula
![]() $\varphi$
.
$\varphi$
.
3.3 Dependence logic
First observe that if
![]() $\varphi$
is a
$\varphi$
is a
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-sentence, then the problem
${{\mathcal{FO}(\mathsf{dep})}}$
-sentence, then the problem
![]() $\text{p-} \mathrm{WT}_\varphi$
is
$\text{p-} \mathrm{WT}_\varphi$
is
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
-complete. This is due to the reason that the data complexity of certain
${{\mathbf{para}}}{{\mathbf{NP}}}$
-complete. This is due to the reason that the data complexity of certain
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-sentences is already
${{\mathcal{FO}(\mathsf{dep})}}$
-sentences is already
![]() ${{\mathbf{NP}}}$
-complete (Väänänen Reference Väänänen2007).
${{\mathbf{NP}}}$
-complete (Väänänen Reference Väänänen2007).
Theorem 18. There is a
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-sentence
${{\mathcal{FO}(\mathsf{dep})}}$
-sentence
![]() $\varphi$
, such that the problem
$\varphi$
, such that the problem
![]() $\text{p-}\mathrm{WT}_\varphi$
is
$\text{p-}\mathrm{WT}_\varphi$
is
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
-complete.
${{\mathbf{para}}}{{\mathbf{NP}}}$
-complete.
Proof. Recall that by the locality property a
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-sentence
${{\mathcal{FO}(\mathsf{dep})}}$
-sentence
![]() $\varphi$
is satisfied by all teams T over
$\varphi$
is satisfied by all teams T over
![]() $\mathcal{A}$
if and only if
$\mathcal{A}$
if and only if
![]() $\mathcal{A},T^*\models \varphi$
for some nonempty team
$\mathcal{A},T^*\models \varphi$
for some nonempty team
![]() $T^*$
. Let now
$T^*$
. Let now
![]() $\varphi$
be a sentence of dependence logic expressing an
$\varphi$
be a sentence of dependence logic expressing an
![]() ${{\mathbf{NP}}}$
-complete problem. Then, for any fixed
${{\mathbf{NP}}}$
-complete problem. Then, for any fixed
![]() $k>0$
, the problem: given a model
$k>0$
, the problem: given a model
![]() $\mathcal{A}$
, determine whether there exists a team with k elements satisfying
$\mathcal{A}$
, determine whether there exists a team with k elements satisfying
![]() $\varphi$
in
$\varphi$
in
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() ${{\mathbf{NP}}}$
-complete. This immediately implies that the problem
${{\mathbf{NP}}}$
-complete. This immediately implies that the problem
![]() $\text{p-} \mathrm{WT}_\varphi$
is
$\text{p-} \mathrm{WT}_\varphi$
is
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
-complete.
${{\mathbf{para}}}{{\mathbf{NP}}}$
-complete.
Now, we relate the
![]() ${{\mathbf{W}}}$
-hierarchy to the weighted definability for dependence logic. This also settles the complexity of
${{\mathbf{W}}}$
-hierarchy to the weighted definability for dependence logic. This also settles the complexity of
![]() $\text{p-} \mathrm{WT}{}$
for
$\text{p-} \mathrm{WT}{}$
for
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formulas. In the following, we prove that already one universal quantifier is enough in
${{\mathcal{FO}(\mathsf{dep})}}$
-formulas. In the following, we prove that already one universal quantifier is enough in
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
to define
${{\mathcal{FO}(\mathsf{dep})}}$
to define
![]() ${{\mathbf{W}[1]}}$
-complete problems.
${{\mathbf{W}[1]}}$
-complete problems.
Theorem 19. There is a
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula
${{\mathcal{FO}(\mathsf{dep})}}$
-formula
![]() $\varphi$
with only one universal quantifier such that the problem
$\varphi$
with only one universal quantifier such that the problem
![]() $\text{p-}\mathrm{WT}_\varphi$
is
$\text{p-}\mathrm{WT}_\varphi$
is
![]() ${{\mathbf{W}[1]}}$
-complete.
${{\mathbf{W}[1]}}$
-complete.
Proof. We present a reduction from the
![]() ${{\mathbf{W}[1]}}$
-complete problem
${{\mathbf{W}[1]}}$
-complete problem
![]() $\text{p-}{{\small{IndependentSet}}}$
to
$\text{p-}{{\small{IndependentSet}}}$
to
![]() $\text{p-}\mathrm{WT}_\varphi$
such that
$\text{p-}\mathrm{WT}_\varphi$
such that
![]() $\varphi$
is
$\varphi$
is
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula with only one universal quantifier. An input to
${{\mathcal{FO}(\mathsf{dep})}}$
-formula with only one universal quantifier. An input to ![]() is a graph
is a graph
![]() $\mathcal{G}\mathrel{\mathop:}= (V,E)$
and a number
$\mathcal{G}\mathrel{\mathop:}= (V,E)$
and a number
![]() $k\in \mathbb N$
. The question is whether there is a set S of size k in
$k\in \mathbb N$
. The question is whether there is a set S of size k in
![]() $\mathcal{G}$
such that
$\mathcal{G}$
such that
![]() $(a,b)\not \in E$
for every
$(a,b)\not \in E$
for every
![]() $a,b\in S$
. We let
$a,b\in S$
. We let
![]() $\tau \mathrel{\mathop:}= \{N^1, P^1, I^2\}$
as our vocabulary where N,P are unary relations and I is a binary relation symbol. Moreover, the
$\tau \mathrel{\mathop:}= \{N^1, P^1, I^2\}$
as our vocabulary where N,P are unary relations and I is a binary relation symbol. Moreover, the
![]() $\tau$
-structure
$\tau$
-structure
![]() $\mathcal{A}$
is such that:
$\mathcal{A}$
is such that:
![]() $\mathrm{dom}(\mathcal{A})\mathrel{\mathop:}= V\cup E$
,
$\mathrm{dom}(\mathcal{A})\mathrel{\mathop:}= V\cup E$
,
![]() $N^\mathcal{A}\mathrel{\mathop:}= V, P^\mathcal{A}\mathrel{\mathop:}= E$
and
$N^\mathcal{A}\mathrel{\mathop:}= V, P^\mathcal{A}\mathrel{\mathop:}= E$
and
![]() $I^\mathcal{A}$
simulates the edge relation
$I^\mathcal{A}$
simulates the edge relation
![]() $E^\mathcal{G}$
. That is,
$E^\mathcal{G}$
. That is,
![]() $I\mathrel{\mathop:}=\{\,(a,b), (c,b)\mid a,c\in V,\text{ and } b\in P \text{ denotes the edge }(a,c)\in E\,\}$
. Finally, we define a
$I\mathrel{\mathop:}=\{\,(a,b), (c,b)\mid a,c\in V,\text{ and } b\in P \text{ denotes the edge }(a,c)\in E\,\}$
. Finally, we define a
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula
${{\mathcal{FO}(\mathsf{dep})}}$
-formula
![]() $\varphi$
over a single free variable x as in the following.
$\varphi$
over a single free variable x as in the following.
The correctness of our reduction is established via the following claim and also shows that the formula
![]() $\varphi$
is, in fact, equivalent to the familiar definition of independent sets via a
$\varphi$
is, in fact, equivalent to the familiar definition of independent sets via a
![]() ${{\mathrm{\Pi}_{1}}}$
-formula; hence,
${{\mathrm{\Pi}_{1}}}$
-formula; hence,
![]() $\text{p-}\mathrm{WT}_\varphi$
is
$\text{p-}\mathrm{WT}_\varphi$
is
![]() ${{\mathbf{W}[1]}}$
-complete.
${{\mathbf{W}[1]}}$
-complete.
Claim 20. There is a team T over x in
![]() $\mathcal{A}$
such that
$\mathcal{A}$
such that
![]() $|T|=k$
and
$|T|=k$
and
![]() $\mathcal{A},T\models \varphi$
if and only if there is an independent set in
$\mathcal{A},T\models \varphi$
if and only if there is an independent set in
![]() $\mathcal{G}$
of size k.
$\mathcal{G}$
of size k.
It remains to prove the claim. Suppose that
![]() $T=\{\,s_i\mid i\leq k\,\}$
is a team over x for
$T=\{\,s_i\mid i\leq k\,\}$
is a team over x for
![]() $\varphi$
such that
$\varphi$
such that
![]() $s_i(x)=a_i$
for
$s_i(x)=a_i$
for
![]() $a_i\in A$
. Moreover, let
$a_i\in A$
. Moreover, let
![]() $T'=\{\,s_{i,j}\mid i\leq k,j\leq |\mathcal{A}|\,\}$
denote the supplemented team, that is,
$T'=\{\,s_{i,j}\mid i\leq k,j\leq |\mathcal{A}|\,\}$
denote the supplemented team, that is,
![]() $s_{i,j}(x)=a_i$
and
$s_{i,j}(x)=a_i$
and
![]() $s_{i,j}(y)=a_j$
for every
$s_{i,j}(y)=a_j$
for every
![]() $a_j\in \mathcal{A}$
. We prove that
$a_j\in \mathcal{A}$
. We prove that
![]() $S=\{a_i \mid \exists s\in T, s(x)=a_i \}$
constitutes an independent set in
$S=\{a_i \mid \exists s\in T, s(x)=a_i \}$
constitutes an independent set in
![]() $\mathcal{G}$
. Let
$\mathcal{G}$
. Let
![]() $a_i,a_j\in S$
, then there are
$a_i,a_j\in S$
, then there are
![]() $s_i,s_j \in T$
such that
$s_i,s_j \in T$
such that
![]() $s_i(x)=a_i$
,
$s_i(x)=a_i$
,
![]() $s_j(x)=a_j$
. Suppose further that
$s_j(x)=a_j$
. Suppose further that
![]() $(a_i,a_j)=e\in E^\mathcal{G}$
. Then, by our construction, there are
$(a_i,a_j)=e\in E^\mathcal{G}$
. Then, by our construction, there are
![]() $s_{i,j},s_{j,j}\in T'$
such that
$s_{i,j},s_{j,j}\in T'$
such that
![]() $s_{i,j}(xy)=a_ia_j$
and
$s_{i,j}(xy)=a_ia_j$
and
![]() $s_{j,j}= a_ja_j$
. Moreover, the pair
$s_{j,j}= a_ja_j$
. Moreover, the pair
![]() $s_{i,j},s_{j,j}$
cannot be in the subteam for the first disjunct since e is an edge and
$s_{i,j},s_{j,j}$
cannot be in the subteam for the first disjunct since e is an edge and
![]() $T'\models P(e)$
; it can also not belong to the subteam for the second disjunct since both
$T'\models P(e)$
; it can also not belong to the subteam for the second disjunct since both
![]() $a_i$
and
$a_i$
and
![]() $a_j$
appear in the edge e. As a result,
$a_j$
appear in the edge e. As a result,
![]() $s_{i,j},s_{j,j}$
must be in the subteam for the third disjunct, but then it cannot satisfy the atom
$s_{i,j},s_{j,j}$
must be in the subteam for the third disjunct, but then it cannot satisfy the atom
![]() ${\mathsf{dep}}({y};\,{x})$
since
${\mathsf{dep}}({y};\,{x})$
since
![]() $s_{i,j}(y)= s_{j,j}(y)$
and
$s_{i,j}(y)= s_{j,j}(y)$
and
![]() $s_{i,j}(x)\not= s_{j,j}(x)$
. Consequently,
$s_{i,j}(x)\not= s_{j,j}(x)$
. Consequently,
![]() $T'\not\models (\neg P(y)\lor \neg I(x,y)\lor {\mathsf{dep}}({y};{x}))$
and
$T'\not\models (\neg P(y)\lor \neg I(x,y)\lor {\mathsf{dep}}({y};{x}))$
and
![]() $T\not\models \varphi$
, which is a contradiction.
$T\not\models \varphi$
, which is a contradiction.
Conversely, if there is an independent set S of size k in
![]() $\mathcal{G}$
then we prove that
$\mathcal{G}$
then we prove that
![]() $T\models \varphi(x)$
for
$T\models \varphi(x)$
for
![]() $T =\{s_i \mid i\leq k, s_i(x)\in S\}$
. Clearly, the supplemented team T’ over
$T =\{s_i \mid i\leq k, s_i(x)\in S\}$
. Clearly, the supplemented team T’ over
![]() $\{x,y\}$
has the following effect: for every y that corresponds to an edge e between elements
$\{x,y\}$
has the following effect: for every y that corresponds to an edge e between elements
![]() $a_i,a_j\in A$
, at most one of its endpoint
$a_i,a_j\in A$
, at most one of its endpoint
![]() $a_i$
or
$a_i$
or
![]() $a_j$
is in T, which is the case if and only if S is in independent set.
$a_j$
is in T, which is the case if and only if S is in independent set.
Once again, we prove the next lemma that generalizes the previous theorem to arbitrary levels of the
![]() ${{\mathbf{W}}}$
-hierarchy using the circuit representation of a formula (Def. 14).
${{\mathbf{W}}}$
-hierarchy using the circuit representation of a formula (Def. 14).
Lemma 21. Let
![]() $t\in \mathbb{N}$
. Then there exists a fixed formula
$t\in \mathbb{N}$
. Then there exists a fixed formula
![]() $\varphi_t\in {{\mathcal{FO}(\mathsf{dep})}}$
with one free variable z such that for all
$\varphi_t\in {{\mathcal{FO}(\mathsf{dep})}}$
with one free variable z such that for all
![]() $\psi \in \Gamma^{-}_{t,d}$
and
$\psi \in \Gamma^{-}_{t,d}$
and
![]() $k\ge 1$
:
$k\ge 1$
:
![]() $\psi$
has a satisfying assignment of weight k if and only if
$\psi$
has a satisfying assignment of weight k if and only if
![]() $A_{\psi},T\models \varphi_t$
, for some team T of cardinality k.
$A_{\psi},T\models \varphi_t$
, for some team T of cardinality k.
Proof. Without loss of generality, we assume that
![]() $d=1$
. Otherwise, the presented proof will easily generalize to larger values of d by a disjunction/conjunction of arity d. By the results of Kontinen and Väänänen (Reference Kontinen and Väänänen2009), it suffices to show that the required formula can be expressed by a first-order sentence
$d=1$
. Otherwise, the presented proof will easily generalize to larger values of d by a disjunction/conjunction of arity d. By the results of Kontinen and Väänänen (Reference Kontinen and Väänänen2009), it suffices to show that the required formula can be expressed by a first-order sentence
![]() $\theta(S)$
in which the relation symbol S occurs only negatively. Then the existence of
$\theta(S)$
in which the relation symbol S occurs only negatively. Then the existence of
![]() $\varphi_t(z)$
satisfying
$\varphi_t(z)$
satisfying
for all nonempty T and
![]() $\mathrm{rel}(T)=S$
follows. Now (for t even) it is easy to check that
$\mathrm{rel}(T)=S$
follows. Now (for t even) it is easy to check that
![]() $\theta(S)$
can be expressed as follows:
$\theta(S)$
can be expressed as follows:
In the case t is odd the conjunction after
![]() $E(x_{t-1},x_t)$
has to be replaced by an implication. The relation symbol S appears only once in the formula and this appearance is negative.
$E(x_{t-1},x_t)$
has to be replaced by an implication. The relation symbol S appears only once in the formula and this appearance is negative.
Notice further that the translation of the formula
![]() $\theta$
to a
$\theta$
to a
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula only introduces dependence atoms and, in particular, does not require any further quantification. Therefore, the following corollary (with proof analogous to Corollary 16) follows. Recall that every dependence logic formula can be put into the
${{\mathcal{FO}(\mathsf{dep})}}$
-formula only introduces dependence atoms and, in particular, does not require any further quantification. Therefore, the following corollary (with proof analogous to Corollary 16) follows. Recall that every dependence logic formula can be put into the
![]() $\forall\exists$
-normal form. As a result, tracking the quantifier prefix in Lemma 21 is not useful and we get the much stronger statement that the whole
$\forall\exists$
-normal form. As a result, tracking the quantifier prefix in Lemma 21 is not useful and we get the much stronger statement that the whole
![]() ${{\mathbf{W}}}$
-hierarchy is already contained in
${{\mathbf{W}}}$
-hierarchy is already contained in
![]() ${{{{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Pi}_{2}}}}}$
. Yet, there is a trade-off one has to keep in mind while reaching this normal form: each existential quantifier (beyond the first) then induces a dependence atom in that case.
${{{{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Pi}_{2}}}}}$
. Yet, there is a trade-off one has to keep in mind while reaching this normal form: each existential quantifier (beyond the first) then induces a dependence atom in that case.
Corollary 22. Let
![]() $t\geq 1$
be odd. Then there is an
$t\geq 1$
be odd. Then there is an
![]() ${{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Pi}_{2}}}$
-formula
${{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Pi}_{2}}}$
-formula
![]() $\varphi_t$
for which the problem
$\varphi_t$
for which the problem
![]() $\text{p-}\mathrm{WT}_{\varphi_t}$
is
$\text{p-}\mathrm{WT}_{\varphi_t}$
is
![]() ${{\mathbf{W}[t]}}$
-complete. Moreover,
${{\mathbf{W}[t]}}$
-complete. Moreover,
![]() $\bigcup_{t\ge1}{{\mathbf{W}[t]}} \subseteq [\text{p-}\mathrm{WT}\text-{{{{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Pi}_{2}}}}}]^{{{\mathbf{FPT}}}}$
.
$\bigcup_{t\ge1}{{\mathbf{W}[t]}} \subseteq [\text{p-}\mathrm{WT}\text-{{{{\mathcal{FO}(\mathsf{dep})}}\text-{{\mathrm{\Pi}_{2}}}}}]^{{{\mathbf{FPT}}}}$
.
Finally,
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
captures the class
${{\mathcal{FO}(\mathsf{dep})}}$
captures the class
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
as established below.
${{\mathbf{para}}}{{\mathbf{NP}}}$
as established below.
Theorem 23.
![]() $[\text{p-}\mathrm{WT}\text-{{\mathcal{FO}(\mathsf{dep})}}]^{{{\mathbf{FPT}}}}={{\mathbf{para}}}{{\mathbf{NP}}}$
.
$[\text{p-}\mathrm{WT}\text-{{\mathcal{FO}(\mathsf{dep})}}]^{{{\mathbf{FPT}}}}={{\mathbf{para}}}{{\mathbf{NP}}}$
.
Proof. Hardness follows from Theorem 18. For membership, we present the following nondeterministic algorithm that runs in polynomial time in the size of
![]() $\mathrm{dom}(\mathcal{A})$
. Notice that since the formula is fixed, we have fixed many connectives including disjunctions and quantifiers. The idea of the algorithm is that it guesses a team T of size k, as well as, a sequence
$\mathrm{dom}(\mathcal{A})$
. Notice that since the formula is fixed, we have fixed many connectives including disjunctions and quantifiers. The idea of the algorithm is that it guesses a team T of size k, as well as, a sequence
![]() $T_i$
for
$T_i$
for
![]() $i\in \mathbb N$
of teams which corresponds to the operations of supplementation and splits according to the formula
$i\in \mathbb N$
of teams which corresponds to the operations of supplementation and splits according to the formula
![]() $\varphi$
. In other words, let
$\varphi$
. In other words, let
![]() $\varphi=Q_1x_1Q_2x_2\dots Q_\ell x_\ell \psi$
be an
$\varphi=Q_1x_1Q_2x_2\dots Q_\ell x_\ell \psi$
be an
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula, where
${{\mathcal{FO}(\mathsf{dep})}}$
-formula, where
![]() $Q\in\{\forall,\exists\}$
and
$Q\in\{\forall,\exists\}$
and
![]() $\psi$
is quantifier free. Then the algorithm performs the following steps.
$\psi$
is quantifier free. Then the algorithm performs the following steps.
-
Guess a team T of size k over
 ${{\mathrm{Fr}}}(\varphi)$
in
${{\mathrm{Fr}}}(\varphi)$
in
 $\mathcal{A}$
.
$\mathcal{A}$
. -
For each
 $i\in \{\ell,\dots,1\}$
, guess a team
$i\in \{\ell,\dots,1\}$
, guess a team
 $T_i$
over
$T_i$
over
 ${{\mathrm{Fr}}}(\varphi)\cup\{x_\ell,\dots,x_i\}$
in an inside-out order of quantification, such that: if
${{\mathrm{Fr}}}(\varphi)\cup\{x_\ell,\dots,x_i\}$
in an inside-out order of quantification, such that: if
 $Q_i = \forall$
, then
$Q_i = \forall$
, then
 $T_i = P^x_{\mathcal{A}}$
and if
$T_i = P^x_{\mathcal{A}}$
and if
 $Q_i = \exists$
, then
$Q_i = \exists$
, then
 $T_i = P^x_{f}$
where
$T_i = P^x_{f}$
where
 $f\colon P\rightarrow \mathcal P(A)\setminus\emptyset $
and
$f\colon P\rightarrow \mathcal P(A)\setminus\emptyset $
and
 $P=T_{i+1}$
(we let
$P=T_{i+1}$
(we let
 $T_{\ell+1}=T$
).Notice that
$T_{\ell+1}=T$
).Notice that
 $|T_i| =|T_{i+1}|$
if
$|T_i| =|T_{i+1}|$
if
 $Q_i=\exists$
(because
$Q_i=\exists$
(because
 ${{\mathcal{FO}(\mathsf{dep})}}$
is downward closed) and
${{\mathcal{FO}(\mathsf{dep})}}$
is downward closed) and
 $|T_i| =|T_{i+1}|\cdot |A|$
otherwise. As a result, we have that
$|T_i| =|T_{i+1}|\cdot |A|$
otherwise. As a result, we have that
 $|T_i| \leq k\cdot |A|^{\ell-i}$
and the size of the team
$|T_i| \leq k\cdot |A|^{\ell-i}$
and the size of the team
 $|T_1|$
is bounded by
$|T_1|$
is bounded by
 $k\cdot |A|^{\ell}$
.Once the team
$k\cdot |A|^{\ell}$
.Once the team
 $T_1$
has been guessed, the algorithm needs to determine whether
$T_1$
has been guessed, the algorithm needs to determine whether
 $T_1 \models \psi$
. Since the data complexity of
$T_1 \models \psi$
. Since the data complexity of
 ${{\mathcal{FO}(\mathsf{dep})}}$
is still
${{\mathcal{FO}(\mathsf{dep})}}$
is still
 ${{\mathbf{NP}}}$
-complete for quantifier free formulas, this step is also nontrivial. Nevertheless, we can list recursively all the subformulas of
${{\mathbf{NP}}}$
-complete for quantifier free formulas, this step is also nontrivial. Nevertheless, we can list recursively all the subformulas of
 $\psi$
in terms of its syntax tree. This helps in labeling a subteams of
$\psi$
in terms of its syntax tree. This helps in labeling a subteams of
 $T_1$
according to the connectives of
$T_1$
according to the connectives of
 $\psi$
.
$\psi$
. -
Guess subteams for subformulas in a top-down order of the syntax tree of
 $\psi$
. To be precise, let
$\psi$
. To be precise, let
 $T_\psi\mathrel{\mathop:}= T_1 $
. Then, for each subformula
$T_\psi\mathrel{\mathop:}= T_1 $
. Then, for each subformula
 $\alpha = \beta\land \gamma$
of
$\alpha = \beta\land \gamma$
of
 $\psi$
, let
$\psi$
, let
 $T_\beta=T_\gamma = T_\alpha$
, and for each
$T_\beta=T_\gamma = T_\alpha$
, and for each
 $\alpha = \beta\lor \gamma$
, let
$\alpha = \beta\lor \gamma$
, let
 $T_\beta\cup T_\gamma = T_\alpha$
.Clearly, the size of the subteam
$T_\beta\cup T_\gamma = T_\alpha$
.Clearly, the size of the subteam
 $T_\alpha$
for each
$T_\alpha$
for each
 $\alpha$
is atmost
$\alpha$
is atmost
 $k\cdot |A|^\ell$
.
$k\cdot |A|^\ell$
. -
Accept if
 $T_\alpha\models \alpha$
for each atomic subformula
$T_\alpha\models \alpha$
for each atomic subformula
 $\alpha$
of
$\alpha$
of
 $\varphi$
.
$\varphi$
.
Notice that for atomic formulas the truth evaluation
![]() $T_\alpha\models \alpha$
can be determined in polynomial time. Moreover, the intermediate steps including the verification of the team supplementation can also be performed in polynomial time. Finally, the correctness follows from the fact that the algorithm simulates the truth evaluation (see Def. 8) for
$T_\alpha\models \alpha$
can be determined in polynomial time. Moreover, the intermediate steps including the verification of the team supplementation can also be performed in polynomial time. Finally, the correctness follows from the fact that the algorithm simulates the truth evaluation (see Def. 8) for
![]() $\varphi$
. This results in
$\varphi$
. This results in
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
-membership of
${{\mathbf{para}}}{{\mathbf{NP}}}$
-membership of
![]() $\mathrm{WT}_\varphi$
for a fixed
$\mathrm{WT}_\varphi$
for a fixed
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
-formula
${{\mathcal{FO}(\mathsf{dep})}}$
-formula
![]() $\varphi$
.
$\varphi$
.
3.4 Independence logic
In this section, we turn to independence logic. The following theorem is obtained from the results in the previous sections and the fact that any
![]() ${{\mathcal{ESO}}}$
-sentence
${{\mathcal{ESO}}}$
-sentence
![]() $\psi(S)$
(with an extra relation encoding the team) can be represented by an independence logic formula (Galliani Reference Galliani2012). It is worth remarking that
$\psi(S)$
(with an extra relation encoding the team) can be represented by an independence logic formula (Galliani Reference Galliani2012). It is worth remarking that
![]() ${{\mathcal{FO}(\bot)}}$
has the empty team property and can therefore only represent an
${{\mathcal{FO}(\bot)}}$
has the empty team property and can therefore only represent an
![]() ${{\mathcal{ESO}}}$
-sentence
${{\mathcal{ESO}}}$
-sentence
![]() $\psi(S)$
if
$\psi(S)$
if
![]() $\psi$
is also true for the empty relation. This is unproblematic since we implicitly assume that
$\psi$
is also true for the empty relation. This is unproblematic since we implicitly assume that
![]() $k\geq 1$
.
$k\geq 1$
.
Theorem 24.
-
(1) For all
 $t\in\mathbb N$
there is an
$t\in\mathbb N$
there is an
 ${{\mathcal{FO}(\bot)}}$
-formula
${{\mathcal{FO}(\bot)}}$
-formula
 $\varphi_t$
such that
$\varphi_t$
such that
 $\text{p-}\mathrm{WT}_{\varphi_t}$
is
$\text{p-}\mathrm{WT}_{\varphi_t}$
is
 ${{\mathbf{W}[t]}}$
-complete.
${{\mathbf{W}[t]}}$
-complete. -
(2) There is an
 ${{\mathcal{FO}(\bot)}}$
-formula
${{\mathcal{FO}(\bot)}}$
-formula
 $\varphi_w$
such that
$\varphi_w$
such that
 $\text{p-}\mathrm{WT}_{\varphi_w}$
is
$\text{p-}\mathrm{WT}_{\varphi_w}$
is
 ${{\mathbf{W}[{{\mathbf{P}}}]}}$
-complete.
${{\mathbf{W}[{{\mathbf{P}}}]}}$
-complete.
-
(3) There is a
 ${{\mathcal{FO}(\bot)}}$
-sentence
${{\mathcal{FO}(\bot)}}$
-sentence
 $\varphi$
, such that the problem
$\varphi$
, such that the problem
 $\text{p-}\mathrm{WT}_\varphi$
is
$\text{p-}\mathrm{WT}_\varphi$
is
 ${{\mathbf{para}}}{{\mathbf{NP}}}$
-complete.
${{\mathbf{para}}}{{\mathbf{NP}}}$
-complete. -
(4)
 $[\text{p-}\mathrm{WT}\text-{{\mathcal{FO}(\bot)}}]^{{{\mathbf{FPT}}}}={{\mathbf{para}}}{{\mathbf{NP}}}$
.
$[\text{p-}\mathrm{WT}\text-{{\mathcal{FO}(\bot)}}]^{{{\mathbf{FPT}}}}={{\mathbf{para}}}{{\mathbf{NP}}}$
.
Proof. The first and third claim follow immediately from the fact that the logics
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
and
${{\mathcal{FO}(\mathsf{dep})}}$
and
![]() ${{\mathcal{FO}(\subseteq)}}$
are sublogics of
${{\mathcal{FO}(\subseteq)}}$
are sublogics of
![]() ${{\mathcal{FO}(\bot)}}$
(Galliani Reference Galliani2012) vtogether with Theorem 23. The containment of
${{\mathcal{FO}(\bot)}}$
(Galliani Reference Galliani2012) vtogether with Theorem 23. The containment of
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
(resp.,
${{\mathcal{FO}(\mathsf{dep})}}$
(resp.,
![]() ${{\mathcal{FO}(\subseteq)}}$
) inside
${{\mathcal{FO}(\subseteq)}}$
) inside
![]() ${{\mathcal{FO}(\bot)}}$
yields the results for odd (even)
${{\mathcal{FO}(\bot)}}$
yields the results for odd (even)
![]() $t\in \mathbb N$
in conjunction with Corollary 22 (Cor. 16), thereby proving the first claim for all
$t\in \mathbb N$
in conjunction with Corollary 22 (Cor. 16), thereby proving the first claim for all
![]() $t\geq 1$
.
$t\geq 1$
.
For the second claim, we use the fact that
![]() $\text{p-}{{\mathrm{WSAT}}}(\text{CIRC}^+)$
is
$\text{p-}{{\mathrm{WSAT}}}(\text{CIRC}^+)$
is
![]() ${{\mathbf{W}[{{\mathbf{P}}}]}}$
-complete (Flum and Grohe Reference Flum and Grohe2006, Thm. 3.14), where CIRC
${{\mathbf{W}[{{\mathbf{P}}}]}}$
-complete (Flum and Grohe Reference Flum and Grohe2006, Thm. 3.14), where CIRC
![]() $^+$
is the class of negation-free propositional formulas encoded as monotone Boolean circuits. Note that the circuit value problem can be readily expressed by an
$^+$
is the class of negation-free propositional formulas encoded as monotone Boolean circuits. Note that the circuit value problem can be readily expressed by an
![]() ${{\mathcal{ESO}}}$
-sentence
${{\mathcal{ESO}}}$
-sentence
![]() $\psi(S)$
, where S represents an input for the circuit. More precisely, assume we a given a DAG (A,E,D,K,I,o) encoding a Boolean circuit. Here A is the set of nodes/gates, E is the edge relation,
$\psi(S)$
, where S represents an input for the circuit. More precisely, assume we a given a DAG (A,E,D,K,I,o) encoding a Boolean circuit. Here A is the set of nodes/gates, E is the edge relation,
![]() $I\subseteq A$
are the input gates of the circuit, o is the unique output,
$I\subseteq A$
are the input gates of the circuit, o is the unique output,
![]() $D\subseteq A$
is the set of OR-gates, and
$D\subseteq A$
is the set of OR-gates, and
![]() $K\subseteq A$
is the set of AND-gates. A Boolean input for the circuit is represented by a subset
$K\subseteq A$
is the set of AND-gates. A Boolean input for the circuit is represented by a subset
![]() $S\subseteq I$
, i.e., a gate g gets input 1 if and only if
$S\subseteq I$
, i.e., a gate g gets input 1 if and only if
![]() $g\in S$
. Now in
$g\in S$
. Now in
![]() ${{\mathcal{ESO}}}$
we can existentially quantify a proof tree witnessing the circuit accepting the input S. In other words, we quantify a subset
${{\mathcal{ESO}}}$
we can existentially quantify a proof tree witnessing the circuit accepting the input S. In other words, we quantify a subset
![]() $P\subseteq A$
such that
$P\subseteq A$
such that
-
 $o\in A$
,
$o\in A$
, -
 $P\cap I=S$
,
$P\cap I=S$
, -
for all
 $g\in P\cap D$
there exists at least one
$g\in P\cap D$
there exists at least one
 $g'\in P$
such that E(g’,g),
$g'\in P$
such that E(g’,g), -
for all
 $g\in P\cap K$
and all g’, if E(g’,g) then
$g\in P\cap K$
and all g’, if E(g’,g) then
 $g'\in P$
.
$g'\in P$
.
It is straightforward to check that the above conditions can be expressed in first-order logic.
Finally, the hardness for the last claim follows again from the fact that
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
is a sublogic of
${{\mathcal{FO}(\mathsf{dep})}}$
is a sublogic of
![]() ${{\mathcal{FO}(\bot)}}$
and the membership proof is analogous to that of Theorem 23.
${{\mathcal{FO}(\bot)}}$
and the membership proof is analogous to that of Theorem 23.
4. Conclusion
We have defined and studied the parameterized complexity of weighted team definability with respect to formulas of several team-based logics. Our results show that for plain first-order formulas weighted team definability differs greatly from weighted Fagin definability; the former being computationally much simpler. For dependence, independence, and inclusion logic formulas, the complexity of weighted team definability ranges between the classes
![]() ${{\mathbf{W}[t]}}$
and
${{\mathbf{W}[t]}}$
and
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
. Now, these results provide a wide range of natural complete problems for the aforementioned complexity classes enriching the landscape in a nontrivial way. Interestingly, the sentences in the considered logics depict different complexities: namely, membership in
${{\mathbf{para}}}{{\mathbf{NP}}}$
. Now, these results provide a wide range of natural complete problems for the aforementioned complexity classes enriching the landscape in a nontrivial way. Interestingly, the sentences in the considered logics depict different complexities: namely, membership in
![]() ${{\mathbf{FPT}}}$
for
${{\mathbf{FPT}}}$
for
![]() ${{\mathcal{FO}(\subseteq)}}$
and
${{\mathcal{FO}(\subseteq)}}$
and
![]() ${{\mathbf{para}}}{{\mathbf{NP}}}$
-completeness for
${{\mathbf{para}}}{{\mathbf{NP}}}$
-completeness for
![]() ${{\mathcal{FO}(\mathsf{dep})}}$
and
${{\mathcal{FO}(\mathsf{dep})}}$
and
![]() ${{\mathcal{FO}(\bot)}}$
. The main open question is whether the converse directions of Corollary 16 or Theorem 17 can be proven, i.e., if one of the inclusions
${{\mathcal{FO}(\bot)}}$
. The main open question is whether the converse directions of Corollary 16 or Theorem 17 can be proven, i.e., if one of the inclusions
![]() $\bigcup_{t\in\mathbb N}{{\mathbf{W}[t]}}\subseteq [\text{p-}\mathrm{WT}\text-{{\mathcal{FO}}}(\subseteq)]^{{{\mathbf{FPT}}}}\subseteq{{\mathbf{W}[{{\mathbf{P}}}]}}$
is in fact an equality.
$\bigcup_{t\in\mathbb N}{{\mathbf{W}[t]}}\subseteq [\text{p-}\mathrm{WT}\text-{{\mathcal{FO}}}(\subseteq)]^{{{\mathbf{FPT}}}}\subseteq{{\mathbf{W}[{{\mathbf{P}}}]}}$
is in fact an equality.
Funding
Juha Kontinen: Partially funded by Academy of Finland grant 338259 Yasir Mahmood: Partially funded by the EU’s Horizon Europe research and innovation programme within project ENEXA (101070305) Arne Meier: Partially funded by DFG grant ME 4279/3-1 Heribert Vollmer: Partially funded by DAAD Project-ID 57570031