Article contents
On the computational complexity of the Dirichlet Problem for Poisson's Equation
Published online by Cambridge University Press: 28 July 2016
Abstract
The last years have seen an increasing interest in classifying (existence claims in) classical mathematical theorems according to their strength. We pursue this goal from the refined perspective of computational complexity. Specifically, we establish that rigorously solving the Dirichlet Problem for Poisson's Equation is in a precise sense ‘complete’ for the complexity class 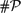 ${\#\mathcal{P}}$ and thus as hard or easy as parametric Riemann integration (Friedman 1984; Ko 1991. Complexity Theory of Real Functions).
${\#\mathcal{P}}$ and thus as hard or easy as parametric Riemann integration (Friedman 1984; Ko 1991. Complexity Theory of Real Functions).
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 27 , Special Issue 8: Continuity, Computability, Constructivity: From Logic to Algorithms 2013 , December 2017 , pp. 1437 - 1465
- Copyright
- Copyright © Cambridge University Press 2016
References
- 7
- Cited by


