Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T11:55:03.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Freely adjoining monoidal duals

Published online by Cambridge University Press:  28 October 2020

Kevin Coulembier ,
Ross Street Open the ORCID record for Ross Street [Opens in a new window]  and
Michel van den Bergh
Kevin Coulembier
Affiliation:
School of Mathematics and Statistics, University of Sydney, Sydney, Australia
Ross Street*
Affiliation:
Department of Mathematics and Statistics, Macquarie University, Sydney, Australia
Michel van den Bergh
Affiliation:
Hasselt University, Department of Mathematics Physics Informatics, Diepenbeek, Belgium
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a monoidal category 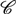$\mathcal C$ with an object J, we construct a monoidal category 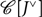$\mathcal C[{J^ \vee }]$ by freely adjoining a right dual 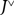${J^ \vee }$ to J. We show that the canonical strong monoidal functor 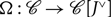$\Omega :\mathcal C \to \mathcal C[{J^ \vee }]$ provides the unit for a biadjunction with the forgetful 2-functor from the 2-category of monoidal categories with a distinguished dual pair to the 2-category of monoidal categories with a distinguished object. We show that 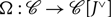$\Omega :\mathcal C \to \mathcal C[{J^ \vee }]$ is fully faithful and provide coend formulas for homs of the form 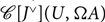$\mathcal C[{J^ \vee }](U,\,\Omega A)$ and 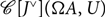$\mathcal C[{J^ \vee }](\Omega A,U)$ for 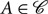$A \in \mathcal C$ and 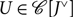$U \in \mathcal C[{J^ \vee }]$. If 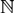${\rm{N}}$ denotes the free strict monoidal category on a single generating object 1, then 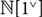${\rm{N[}}{{\rm{1}}^ \vee }{\rm{]}}$ is the free monoidal category Dpr containing a dual pair – ˧ + of objects. As we have the monoidal pseudopushout 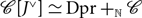$\mathcal C[{J^ \vee }] \simeq {\rm{Dpr}}{{\rm{ + }}_{\rm{N}}}\mathcal C$, it is of interest to have an explicit model of Dpr: we provide both geometric and combinatorial models. We show that the (algebraist’s) simplicial category Δ is a monoidal full subcategory of Dpr and explain the relationship with the free 2-category Adj containing an adjunction. We describe a generalization of Dpr which includes, for example, a combinatorial model Dseq for the free monoidal category containing a duality sequence X0 ˧ X1 ˧ X2 ˧ … of objects. Actually, Dpr is a monoidal full subcategory of Dseq.

Keywords

Autonomizationmonoidal dualstring diagramadjunctionbiadjoint
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 31 , Special Issue 7: The Power Festschrift , August 2021 , pp. 748 - 768
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auderset, C. (1974). Adjonctions et monades au niveau des 2-catégories. Cahiers de Topologie et Géométrie Différentielle Catégoriques 15 3–20.Google Scholar
Batanin, M. A. (1998). Monoidal globular categories as a natural environment for the theory of weak n-categories. Advances in Mathematics 136 39–103.CrossRefGoogle Scholar
Bénabou, J. (1973). Les distributeurs, Univ. Catholique de Louvain, Séminaires de Math. Pure, Rapport No. 33.Google Scholar
Day, B. J. and Pastro, C. (2008). Note on Frobenius monoidal functors. The New York Journal of Mathematics 14 733–742.Google Scholar
Delpeuch, A. (2019). Autonomization of monoidal categories, 25 pp. see arXiv:1411.3827v3.Google Scholar
Eilenberg, S. and Kelly, G. M. (1966). Closed categories. In: Proceedings of the Conference on Categorical Algebra (La Jolla, 1965), Springer-Verlag, Berlin, 421–562.CrossRefGoogle Scholar
Joyal, A. and Street, R. (1988). Planar diagrams and tensor algebra (handwritten notes); see http://web.science.mq.edu.au/~street/PlanarDiags.pdf.Google Scholar
Joyal, A. and Street, R. (1991). The geometry of tensor calculus I. Advances in Mathematics 88 55–112.CrossRefGoogle Scholar
Kan, D. M. (1958). Adjoint functors. Transactions of the American Mathematical Society 87 294–329.CrossRefGoogle Scholar
Kelly, G. M. (1972). Many-Variable Functorial Calculus I, Lecture Notes in Mathematics, vol. 281, Springer-Verlag, Berlin, 66–105.Google Scholar
Lack, S. and Street, R. (2014). Triangulations, orientals, and skew-monoidal categories. Advances in Mathematics 258 351–396.CrossRefGoogle Scholar
(Bill) Lawvere, F. W. (2002). Metric spaces, generalized logic and closed categories. Reprints in Theory and Applications of Categories 1 1–37; originally published as: Rendiconti del Seminario Matematico e Fisico di Milano 53 (1973) 135–166.Google Scholar
Lane, S. M. (1971). Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5, Springer-Verlag, Berlin.Google Scholar
Saavedra Rivano, N. (1972). Catégories Tannakiennes, Lecture Notes in Mathematics, vol. 265, Springer-Verlag, Berlin.Google Scholar
Schanuel, S. and Street, R. (1986). The free adjunction. Cahiers de Topologie et Géométrie Différentielle Catégoriques 27 81–83.Google Scholar
Shum, M. C. (1994). Tortile tensor categories. Journal of Pure and Applied Algebra 93 57–110.CrossRefGoogle Scholar
Street, R. (1980). Fibrations in bicategories. Cahiers de Topologie et Géométrie Différentielle 21 111–160.Google Scholar
Street, R. (1998). Braids among the groups. Seminarberichte aus dem Fachbereich Mathematik 63 (5) 699–703.Google Scholar
Temperley, N. and Lieb, E. (1971). Relations between the ‘percolation’ and ‘colouring’ problem and other graph-theoretical problems associated with regular planar lattices: some exact results for the ‘percolation’ problem. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 322 (1549) 251–280.Google Scholar
Yetter, D. N. (1988). Markov algebras. In: Birman, J. S. and Libgober, A. (eds.) Braids, Contemporary Mathematics, vol. 78, American Mathematical Society, Providence, Rhode Island, 705–730.Google Scholar