Article contents
Fixed points of contractive maps on dcpo's
Published online by Cambridge University Press: 13 May 2013
Abstract
In this paper we study approach structures on dcpo's. A dcpo (X, ≤) will be endowed with several other structures: the Scott topology; an approach structure generated by a collection of weightable quasi metrics on X; and a collection 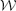 of weights corresponding to the quasi metrics. Understanding the interaction between these structures on X will eventually lead to some fixed-point theorems for the morphisms in the category of approach spaces, which are called contractions. Existing fixed-point theorems on both monotone and non-monotone maps are obtained as special cases.
of weights corresponding to the quasi metrics. Understanding the interaction between these structures on X will eventually lead to some fixed-point theorems for the morphisms in the category of approach spaces, which are called contractions. Existing fixed-point theorems on both monotone and non-monotone maps are obtained as special cases.
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2013
References
- 6
- Cited by


