Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Balan, Adriana
and
Kurz, Alexander
2011.
Algebra and Coalgebra in Computer Science.
Vol. 6859,
Issue. ,
p.
85.
Adámek, Jiří
Milius, Stefan
and
Moss, Lawrence S.
2012.
Coalgebraic Methods in Computer Science.
Vol. 7399,
Issue. ,
p.
51.
Balan, Adriana
Kurz, Alexander
and
Velebil, Jiří
2013.
Algebra and Coalgebra in Computer Science.
Vol. 8089,
Issue. ,
p.
51.
Staton, Sam
2013.
Foundations of Software Science and Computation Structures.
Vol. 7794,
Issue. ,
p.
401.
Chen, Liang-Ting
and
Jung, Achim
2014.
On a Categorical Framework for Coalgebraic Modal Logic.
Electronic Notes in Theoretical Computer Science,
Vol. 308,
Issue. ,
p.
109.
Marti, Johannes
and
Venema, Yde
2015.
Lax extensions of coalgebra functors and their logic.
Journal of Computer and System Sciences,
Vol. 81,
Issue. 5,
p.
880.
Balan, Adriana
Kurz, Alexander
and
Velebil, Jiří
2015.
An institutional approach to positive coalgebraic logic.
Journal of Logic and Computation,
p.
exv074.
Adámek, Jiří
Milius, Stefan
Moss, Lawrence S.
and
Urbat, Henning
2015.
On finitary functors and their presentations.
Journal of Computer and System Sciences,
Vol. 81,
Issue. 5,
p.
813.
Dahlqvist, Fredrik
2016.
Coalgebraic Methods in Computer Science.
Vol. 9608,
Issue. ,
p.
174.


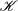 that is equipped by an adjunction
that is equipped by an adjunction 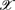 of descent type. We present a class of functors/monads that admit such an equational presentation that involves finitary signatures in
of descent type. We present a class of functors/monads that admit such an equational presentation that involves finitary signatures in 