The costructure–cosemantics adjunction for comodels for computational effects

Abstract

It is well established that equational algebraic theories and the monads they generate can be used to encode computational effects. An important insight of Power and Shkaravska is that comodels of an algebraic theory 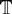$\mathbb{T}$ – i.e., models in the opposite category 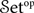$\mathcal{S}\mathrm{et}^{\mathrm{op}}$ – provide a suitable environment for evaluating the computational effects encoded by 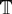$\mathbb{T}$ . As already noted by Power and Shkaravska, taking comodels yields a functor from accessible monads to accessible comonads on 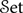$\mathcal{S}\mathrm{et}$ . In this paper, we show that this functor is part of an adjunction – the “costructure–cosemantics adjunction” of the title – and undertake a thorough investigation of its properties. We show that, on the one hand, the cosemantics functor takes its image in what we term the presheaf comonads induced by small categories; and that, on the other, costructure takes its image in the presheaf monads induced by small categories. In particular, the cosemantics comonad of an accessible monad will be induced by an explicitly-described category called its behaviour category that encodes the static and dynamic properties of the comodels. Similarly, the costructure monad of an accessible comonad will be induced by a behaviour category encoding static and dynamic properties of the comonad coalgebras. We tie these results together by showing that the costructure–cosemantics adjunction is idempotent, with fixpoints to either side given precisely by the presheaf monads and comonads. Along the way, we illustrate the value of our results with numerous examples drawn from computation and mathematics.