Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2025-01-02T18:20:02.603Z Has data issue: false hasContentIssue false
  • English
  • Français

An improved primal-dual approximation algorithm for the k-means problem with penalties

Published online by Cambridge University Press:  16 August 2021

Chunying Ren ,
Dachuan Xu ,
Donglei Du  and
Min Li Open the ORCID record for Min Li [Opens in a new window]
Chunying Ren
Affiliation:
Department of Operations Research and Information Engineering, Beijing University of Technology, Beijing 100124, P.R. China
Dachuan Xu
Affiliation:
Department of Operations Research and Information Engineering, Beijing University of Technology, Beijing 100124, P.R. China
Donglei Du
Affiliation:
Faculty of Management, University of New Brunswick, Fredericton, NB E3B 5A3, Canada
Min Li*
Affiliation:
School of Mathematics and Statistics, Shandong Normal University, Jinan 250014, P.R. China
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the k-means problem with penalties, we are given a data set 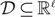$${\cal D} \subseteq \mathbb{R}^\ell $$ of n points where each point 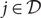$$j \in {\cal D}$$ is associated with a penalty cost pj and an integer k. The goal is to choose a set 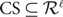$${\rm{C}}S \subseteq {{\cal R}^\ell }$$ with |CS| ≤ k and a penalized subset 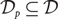$${{\cal D}_p} \subseteq {\cal D}$$ to minimize the sum of the total squared distance from the points in D / Dp to CS and the total penalty cost of points in Dp, namely 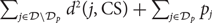$$\sum\nolimits_{j \in {\cal D}\backslash {{\cal D}_p}} {d^2}(j,{\rm{C}}S) + \sum\nolimits_{j \in {{\cal D}_p}} {p_j}$$. We employ the primal-dual technique to give a pseudo-polynomial time algorithm with an approximation ratio of (6.357+ε) for the k-means problem with penalties, improving the previous best approximation ratio 19.849+∊ for this problem given by Feng et al. in Proceedings of FAW (2019).

Keywords

K-means problem with penaltieslinear programapproximation algorithmJV algorithm
Type
Special Issue: Theory and Applications of Models of Computation (TAMC 2020)
Information
Mathematical Structures in Computer Science , Volume 32 , Issue 2: Theory and Applications of Models of Computation (TAMC 2020) , February 2022 , pp. 151 - 163
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†A preliminary version of this paper appeared in Proceedings of the 16th Annual Conference on Theory and Applications of Models of Computation, pp. 377–389, 2020

References

Ahmadian, S., Norouzi-Fard, A., Svensson, O. and Ward, J. (2017). Better guarantees for k-means and Euclidean k-median by primal-dual algorithms. In: Proceedings of FOCS, 61–72.CrossRefGoogle Scholar
Aloise, D., Deshpande, A., Hansen, P. and Popat, P. (2009). NP-hardness of Euclidean sum-of-squares clustering. Machine Learning 75 245–248.CrossRefGoogle Scholar
Arthur, D. and Vassilvitskii, S. (2007). k-means++: the advantages of careful seeding. In: Proceedings of SODA, 1027–1035.Google Scholar
Charikar, M., Khuller, S., Mount, D. M. and Narasimhan, G. (2001). Algorithms for facility location problems with outliers. In: Proceedings of 12th ACM-SIAM Symposium on Discrete Algorithms, 642–651.Google Scholar
Cohen-Addad, V., Klein, P. N. and Mathieu, C. (2019). Local search yields approximation schemes for k-means and k-median in Euclidean and minor-free metrics. SIAM Journal on Computing 48 644–667.CrossRefGoogle Scholar
Drineas, P., Frieze, A., Kannan, R., Vempala, S. and Vinay, V. (2004). Clustering large graphs via the singular value decomposition. Machine Learning 56 9–33.CrossRefGoogle Scholar
Feldman, D., Monemizadeh, M. and Sohler, C. (2007). A PTAS for k– means clustering based on weak coresets. In: Proceedings of the twenty-Third Annual Symposium on Computational Geometry, 11–18.CrossRefGoogle Scholar
Feng, Q., Zhang, Z., Shi, F. and Wang, J. (2019). An improved approximation algorithm for the k-means problem with penalties. In: Proceedings of FAW, 170–181.CrossRefGoogle Scholar
Friggstad, Z., Rezapour, M. and Salavatipour, M. R. (2019). Local search yields a PTAS for k-means in doubling metrics. SIAM Journal on Computing 48 452–480.CrossRefGoogle Scholar
Jain, K. and Vazirani, V. V. (2001). Approximation algorithms for metric facility location and k-median problems using the primal-dual schema and Lagrangian relaxation. Journal of the ACM 48 274–296.CrossRefGoogle Scholar
Ji, S., Xu, D., Guo, L., Li, M. and Zhang, D. (2020). The seeding algorithm for spherical k-means clustering with penalties. Journal of Combinatorial Optimization. doi: 10.1007/s10878-020-00569-1.CrossRefGoogle Scholar
Kanungo, T., Mount, D., Netanyahu, N., Piatko, C. and Silverma, R. (2004). A local search approximation algorithm for k-means clustering. Computational Geometry 28 89–112.CrossRefGoogle Scholar
Li, M. (2020). The bi-criteria seeding algorithms for two variants of k-means problem. Journal of Combinatorial Optimization. doi: 10.1007/s10878-020-00537-9.CrossRefGoogle Scholar
Li, M., Xu, D., Yue, J., Zhang, D. and Zhang, P. (2020). The seeding algorithm for k-means problem with penalties. Journal of Combinatorial Optimization 39 15–32.CrossRefGoogle Scholar
Li, Y., Du, D., Xiu, N. and Xu, D. (2015). Improved approximation algorithms for the facility location problems with linear/submodular penalties. Algorithmica 73 460–482.CrossRefGoogle Scholar
Lloyd, S. (1982). Least squares quantization in PCM. IEEE Transactions on Information Theory 28 129–137.CrossRefGoogle Scholar
Makarychev, K., Makarychev, Y. and Razenshteyn, I. (2019). Performance of Johnson-Lindenstrauss transform for k-means and k-medians clustering. In: Proceedings of STOC, 1027–1038.Google Scholar
Vazirani, V. V. (2001). Approximation Algorithms, Springer-Verlag, Berlin, Heidelberg.Google Scholar
Williamson, D. P. and Shmoys, D. B. (2011). The Design of Approximation Algorithms, Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Zhang, D., Hao, C., Wu, C., Xu, D. and Zhang, Z. (2019). Local search approximation algorithms for the k-means problem with penalties. Journal of Combinatorial Optimization 37 439–453.CrossRefGoogle Scholar