Article contents
Set-syllogistics meet combinatorics
Published online by Cambridge University Press: 11 May 2015
Abstract
This paper considers ∃*∀* prenex sentences of pure first-order predicate calculus with equality. This is the set of formulas which Ramsey's treated in a famous article of 1930. We demonstrate that the satisfiability problem and the problem of existence of arbitrarily large models for these formulas can be reduced to the satisfiability problem for ∃*∀* prenex sentences of Set Theory (in the relators ∈, =).
We present two satisfiability-preserving (in a broad sense) translations Φ ↦ 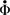 $\dot{\Phi}$ and Φ ↦ Φσ of ∃*∀* sentences from pure logic to well-founded Set Theory, so that if
$\dot{\Phi}$ and Φ ↦ Φσ of ∃*∀* sentences from pure logic to well-founded Set Theory, so that if 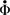 $\dot{\Phi}$ is satisfiable (in the domain of Set Theory) then so is Φ, and if Φσ is satisfiable (again, in the domain of Set Theory) then Φ can be satisfied in arbitrarily large finite structures of pure logic.
$\dot{\Phi}$ is satisfiable (in the domain of Set Theory) then so is Φ, and if Φσ is satisfiable (again, in the domain of Set Theory) then Φ can be satisfied in arbitrarily large finite structures of pure logic.
It turns out that |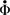 $\dot{\Phi}$| =
$\dot{\Phi}$| = 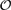 $\mathcal{O}$(|Φ|) and |Φσ| =
$\mathcal{O}$(|Φ|) and |Φσ| = 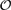 $\mathcal{O}$(|Φ|2).
$\mathcal{O}$(|Φ|2).
Our main result makes use of the fact that ∃*∀* sentences, even though constituting a decidable fragment of Set Theory, offer ways to describe infinite sets. Such a possibility is exploited to glue together infinitely many models of increasing cardinalities of a given ∃*∀* logical formula, within a single pair of infinite sets.
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 27 , Special Issue 2: Special Issue: XIV ICTCS , February 2017 , pp. 296 - 310
- Copyright
- Copyright © Cambridge University Press 2015
References
- 9
- Cited by


