Article contents
Rogers semilattices of punctual numberings
Published online by Cambridge University Press: 29 March 2022
Abstract
The paper works within the framework of punctual computability, which is focused on eliminating unbounded search from constructions in algebra and infinite combinatorics. We study punctual numberings, that is, uniform computations for families S of primitive recursive functions. The punctual reducibility between numberings is induced by primitive recursive functions. This approach gives rise to upper semilattices of degrees, which are called Rogers pr-semilattices. We show that any infinite, uniformly primitive recursive family S induces an infinite Rogers pr-semilattice R. We prove that the semilattice R does not have minimal elements, and every nontrivial interval inside R contains an infinite antichain. In addition, every non-greatest element from R is a part of an infinite antichain. We show that the 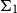 $\Sigma_1$
-fragment of the theory Th(R) is decidable.
$\Sigma_1$
-fragment of the theory Th(R) is decidable.
Keywords
- Type
- Special Issue: Theory and Applications of Models of Computation (TAMC 2020)
- Information
- Mathematical Structures in Computer Science , Volume 32 , Issue 2: Theory and Applications of Models of Computation (TAMC 2020) , February 2022 , pp. 164 - 188
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 2
- Cited by



