No CrossRef data available.
Article contents
Inclusions for partiality
Published online by Cambridge University Press: 02 December 2014
Abstract
In this paper we introduce stable systems of inclusions, which feature chosen arrows A ↪ B to capture the notion that A is a subobject of B, and proposes them as an alternative context to stable systems of monics to discuss partiality. A category C equipped with such a system 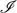 $\mathscr{I}$, called an i-category, is shown to give rise to an associated category ∂(C,
$\mathscr{I}$, called an i-category, is shown to give rise to an associated category ∂(C,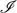 $\mathscr{I}$) of partial maps, which is a split restriction category whose restriction monics are inclusions. This association is the object part of a 2-equivalence between such inclusively split restriction categories and i-categories.
$\mathscr{I}$) of partial maps, which is a split restriction category whose restriction monics are inclusions. This association is the object part of a 2-equivalence between such inclusively split restriction categories and i-categories. 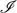 $\mathscr{I}$ determines a stable system of monics
$\mathscr{I}$ determines a stable system of monics 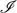 $\mathscr{I}$+ on C, and, conversely, a stable system of monics
$\mathscr{I}$+ on C, and, conversely, a stable system of monics 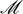 $\mathscr{M}$ on C yields an i-category (C[
$\mathscr{M}$ on C yields an i-category (C[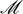 $\mathscr{M}$],
$\mathscr{M}$],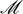 $\mathscr{M}$+), giving a 2-adjunction between i-categories and m-categories. The category of partial maps Par(C,
$\mathscr{M}$+), giving a 2-adjunction between i-categories and m-categories. The category of partial maps Par(C,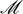 $\mathscr{M}$) is isomorphic to the full subcategory of ∂(C[
$\mathscr{M}$) is isomorphic to the full subcategory of ∂(C[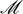 $\mathscr{M}$],
$\mathscr{M}$],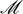 $\mathscr{M}$+) comprising the objects of C, and ∂(C,
$\mathscr{M}$+) comprising the objects of C, and ∂(C,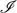 $\mathscr{I}$) ≅ Par(C,
$\mathscr{I}$) ≅ Par(C,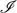 $\mathscr{I}$+).
$\mathscr{I}$+).
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2014


