Article contents
The computational power of timed P systems with active membranes using promoters
Published online by Cambridge University Press: 09 August 2018
Abstract
P systems with active membranes are a class of bioinspired computing models, where the rules are used in the non-deterministic maximally parallel manner. In this paper, first, a new variant of timed P systems with active membranes is proposed, where the application of rules can be regulated by promoters with only two polarizations. Next, we prove that any Turing computable set of numbers can be generated by such a P system in the time-free way. Moreover, we construct a uniform solution to the 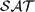 $\mathcal{SAT}$ problem in the framework of such recognizer timed P systems in polynomial time, and the feasibility and effectiveness of the proposed system is demonstrated by an instance. Compared with the existing methods, the P systems constructed in our work require fewer necessary resources and RS-steps, which show that the solution is effective to NP-complete problem.
$\mathcal{SAT}$ problem in the framework of such recognizer timed P systems in polynomial time, and the feasibility and effectiveness of the proposed system is demonstrated by an instance. Compared with the existing methods, the P systems constructed in our work require fewer necessary resources and RS-steps, which show that the solution is effective to NP-complete problem.
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2018
References
- 8
- Cited by


