Research Article
The biaxial surfaces, and the equivalence of binary forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 187-209
-
- Article
- Export citation
On the representations of a number as a sum of squares and certain related identities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-11
-
- Article
- Export citation
The minima of a pair of indefinite, harmonic, binary quadratic forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-96
-
- Article
- Export citation
An extension of a theorem of Mehler's on Hermite polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 12-15
-
- Article
- Export citation
Projective collineations in a space of k-spreads
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 210-223
-
- Article
- Export citation
Totally heterogeneous continua
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 96-103
-
- Article
- Export citation
A general form of the covering principle and relative differentiation of additive functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-110
-
- Article
- Export citation
The elastic stresses produced by the indentation of the plane surface of a semi-infinite elastic solid by a rigid punch
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 16-26
-
- Article
- Export citation
A note on certain stress distributions in isotropic and aeolotropic materials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 224-231
-
- Article
- Export citation
On the reflexion of surface waves by a submerged plane barrier
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-238
-
- Article
- Export citation
On multiple curves. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-117
-
- Article
- Export citation
The symmetrical vibrations of a thin elastic plate
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 27-43
-
- Article
- Export citation
On multiple curves. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-126
-
- Article
- Export citation
Conduction of heat in a slab in contact with well-stirred fluid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-49
-
- Article
- Export citation
Research Notes
The Fourier transform solution of an elastic wave equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 239-243
-
- Article
- Export citation
Research Article
Covariant line complexes of a pair of quadric surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-135
-
- Article
- Export citation
Relativistic wave equations for zero rest-mass
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-56
-
- Article
- Export citation
Proceedings at the meetings
Proceedings at the meetings held during the session 1944–1945: Annual General Meeting
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 244-247
-
- Article
- Export citation
Statement of Accounts
The Cambridge Philosophical Society Statement of Accounts for the Year Ended 31 July 1944: General Account
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 248-249
-
- Article
- Export citation
Research Article
Point-curve correspondences: I. The theory of the base
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-145
-
- Article
- Export citation


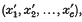 are only considered to be the same solution if
are only considered to be the same solution if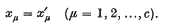
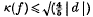 and that this is a ‘best possible’ result.
and that this is a ‘best possible’ result.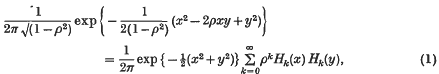
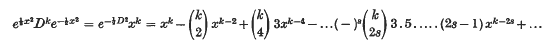
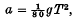 where
where 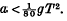 .
.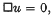 being the relativistic Laplace operator. Analogous questions for any orthogonal group are dealt with in a previous paper, but it was thought that an independent and not too technical treatment for the Lorentz group might be of interest.
being the relativistic Laplace operator. Analogous questions for any orthogonal group are dealt with in a previous paper, but it was thought that an independent and not too technical treatment for the Lorentz group might be of interest.