The quantal quartic oscillator, characterized by two real and two complex conjugate transition points (simple zeros), is studied by means of the phase-integral method developed by Fröman and Fröman, and various quantization conditions are obtained. The main results, obtained in §3·3 and §4, are summarized below.
A correction to the generalized Bohr–Sommerfeld quantization condition, due to the complex conjugate transition points, is obtained from estimates of the. F-matrix for a path passing above the complex conjugate transition points. This quantization condition is closely related to the quantization condition for a double-oscillator. The correction is shown to be rigorously valid when the distance between the real transition points is large compared to the distance between the complex conjugate ones, which may lie at an unspecified distance from each other.
At sufficiently large distances from the cluster of four transition points the solutions of the Schrödinger equation can be characterized by the Stokes constants between anti-Stokes lines emerging from the cluster in six directions towards infinity. There are initially six non-trivial such Stokes constants in the problem under consideration, but, from the results in previous papers by N. Fröman and the present authors, these Stokes constants are linked by a number of algebraic relations, so that one or two Stokes constants suffice to describe the solutions far away from the cluster of transition points. The quantization condition is expressed in terms of these Stokes constants. Approximate values of the relevant Stokes constants are given in the three limiting cases when all four transition points coalesce (and the first-order phase-integral approximation is used), when the distance between the real transition points is sufficiently large (extreme double-oscillator), and in the Bohr-Sommerfeld limit.
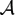 -simple germs from
-simple germs from 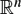 to
to