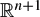Let π be a finite p-group and ${\mathbb{F}_{q}}$ a finite field with q = pn elements. Denote by $\I_{\mathbb{F}_{q}}$ the augmentation ideal of the group ring ${\mathbb{F}_{q}}$[π]. We have found a surprising relation between the abelianization of 1 + $\I_{\mathbb{F}_{q}}$, the Bogomolov multiplier B0(π) of π and the number of conjugacy classes k(π) of π:

$$ \left | (1+\I_{\Fq})_{\ab} \right |=q^{\kk(\pi)-1}|\!\B_0(\pi)|.

$\I_{\mathbb{F}_{q}}$

Williams ((3)) has transformed certain series equations in Legendre functions to Bessel integral equations; his main result being that if

then

and vice versa. (Here, n is written for Williams's n + m. The coefficients an are related to Williams's An by a factor. There is an extra factor 2 in equation (7) in Williams's paper which appears to be an error.)

The problem of finding general types of solution for the steady flow of gases in two dimensions, adiabatically and without friction, does not appear to have received a great deal of attention. An interesting and suggestive treatment of hydrodynamics applied to gases is given in Riemann-Weber's Partielle Differential-Gleichungen, but the application is to pressure propagation. Reference must also be made to a paper by the late Lord Rayleigh, who gave a general differential equation which must be satisfied by the velocity potential ø, but the problem of utilizing this equation does not appear easy.

We say that a real vector bundle ξ over a finite C.W. complex X is stably trivial of type (n, k) or, simply, of type (n, k) if ξ ⊕ kε ≅ nε, where ε denotes a trivial line bundle. The following theorem is an immediate corollary (see (12)) of a theorem of T. Y. Lam ((9), theorem 2).

The results of the present paper were developed some years ago for quite trivial purposes. It seems possible, however, to judge by a recent publication, that they may sooner or later have scientific utility. They have also a certain slight intrinsic interest.

KMS states of a twisted convolution algebra of Schwartz functions on a vector group are classified and related to KMS states of twisted L1-algebras for certain subquotients. The KMS states for the subquotient algebras are also related to Fock states of vector groups. In the particular case of the subquotient Tn × ℤn of ℚ2n this links the Fock space construction of the theta functions with their appearance in KMS states of loop groups and in the Kac character formula.

1. Introduction. A Markov Renewal Process (MRP) with m(<∞) states is one which records at each time t, the number of times a system visits each of the m states up to time t, if the system moves from state to state according to a Markov chain with transition probability matrix P0 = [pij] and if the time required for each successive move is a random variable whose distribution function (d.f.) depends on the two states between which the move is made. Thus, if the system moves from state i to state j, the holding time in the state i has Fij(x) as its d.f. (i, j = 1,2, …, m).

Let T be an operator on a complex Banach space such that sup {‖Tn‖: n ≥ 0} < ∞; such operators are said to be power-bounded. For such an operator one defines the peripheral spectrum to be the set

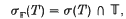
where σ(T) denotes the spectrum of T, and T is the unit circle in ℂ. Esterle proved in [3] that limnn→∞ ‖Tn−Tn+1‖ = 0 provided that ‖T‖ ≤ 1 and σ{T} = {1}. Later Katznelson and Tzafriri [6] proved the same result for power-bounded operators such that σΓ(T) = {1}, and in fact they proved a more general result. More precisely, let 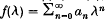be an absolutely convergent Taylor series, i.e. , and assume that f is of spectral synthesis for σΓ(T) (in particular f|σΓ(T) ≡ 0). Then limn→∞ ‖f(T) Tn‖ = 0. Katznelson and Tzafriri prove an analogous result, in which T is replaced by a commuting k-tuple (T1, T2, …, Tk) of contractions. In this case they consider functions of the form f(T1, T2, …, Tk), where f is either an absolutely convergent Taylor series if k is odd, or an element of a smaller algebra if k is even. The result of Katznelson and Tzafriri was further extended in the case of a single contraction T by Esterle, Strouse and Zouakia[4], who consider functions f(T) where f is allowed to be in a more general function algebra. For instance, if T acts on a Hilbert space, they allow f to be an element of the disk algebra.

The purpose of this paper is to investigate the asymptotic behaviour as r → 1− of the integrals

and f is an analytic function on the unit disk Δ which has non-tangential limits at almost every point on ∂Δ. The paper is divided into three parts. In the first part we consider the case where λ ≠ 1/k, in the second the somewhat more delicate case when λ = 1/k and in the third part we concentrate on some problems related to the case λ = k = 1.

The theory of surfaces and of manifolds of higher dimension is greatly handicapped by the lack of exact information concerning the extension of the theorem of Riemann-Roch for curves. Allied to this is the difficulty of finding an expression for the arithmetic genus Pa of primals in terms of their defining elements. This paper seeks to examine certain particular applications of the theorem.

The classical configuration connected with the names of Miquel and Clifford associates with a set of n straight lines in a plane a point called their Miquel point when n is even, and a circle, their Clifford circle, when n is odd. When the number of lines n in a set is even, the omission of these, one at a time, gives n subsets whose associated Clifford circles are concurrent at the Miquel point of the original set; when n is odd, the omission of the lines one at a time gives n subsets whose associated Miquel points are concyclic on the Clifford circle of the original set. To start the chain, it is only necessary to define the Miquel point of two lines as their common point.

Let a cyclic group of odd prime order p act on a ℤ(p)-Poincaré duality space X. We prove a relation between the Witt classes associated to the [ ]p-cohomology rings of the fixed point set of this action and of X. This is applied to show a similar result for actions of finite p-groups on ℤ(p)-homology manifolds.

The purpose of this note is to indicate the relation between (a) the problem of evaporation from a finite area of rectangular shape into a turbulent air stream and of the boundary layer on a flat plate of finite width, and (b) the problem of the boundary layer on a semi-infinite plate and evaporation from an infinite quadrant.

We consider the ground state of a system of three interacting particles of equal mass. An integro-differential equation is obtained for the optimum pair function f in the product wavefunction Ψ(123) = f(12)f(13)f(23). The solution for harmonic forces reproduces the known exact ground state. Approximate analytic solutions are obtained for inverse-square forces, and for a general force law in the semiclassical limit.

If the series Σαn is convergent, it follows that Σαnzn is uniformly convergent in a Stolz angle at z = 1 ((7), p. 229). It was shown in (3) that for the Ces methods (C, α) with α > – 1, and for a certain class of general Nörlund means (containing (C, α) for 0 < α ≤ 1), summability of Σαn implies uniform summability in a Stolz angle at z = 1. In section 2 we prove this theorem for a class of methods which satisfy a mean value property ((6), p. 31), and for a wider class of Nörlund methods which includes (C, α) for all α > 0. An analog is also proved for absolute summability.

The unsteady two-dimensional boundary-layer flows are investigated, using the equations linearized as by Lighthill. It is assumed, unlike separable forms and power functions taken by Sarma, that the perturbations which cause the unsteadiness in the flow are arbitrary functions of the distance along the flow and the time. In addition to the Reynolds number, it is explicitly assumed that the flow for large times is defined by a set of parameters like

ξ = φ/U0, U0(x) and φ (x are functions associated with the main stream in steady flow, λ(x, t) represents a perturbation, t time and x is the distance along the surface. This particular assumption is essentially an idea that is suggested by the work of Sarma. In solving the equations a number of free constants and arbitrary functions are used, which will be specified according to the given physical situation. For large times series solutions are assumed in terms of the above parameters and ultimately sets of differential equations are obtained in a single variable. Thus the theory makes the problem ready for computational work. For small times using the steady state solutions given in this paper, we proceed along the same lines as given in the work of Sarma. The velocity as well as thermal boundary layers are analysed in this paper.

Throughout this paper, G will denote a locally compact, non-discrete, Abelian group (subjected to various conditions) and X wi11 denote the character group of G. All terminology and notation are as in (7). The measure algebra M(G), as is known, is a very complicated entity. We address ourselves here to some novel peculiarities of the subspace Ms(G) of continuous measures in M(G) that are singular with respect to Haar measure λ.

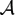All -simple corank-1 germs from 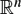to , where n ≠ 4, have an M-deformation, that is a deformation in which the maximal numbers of isolated stable singular points are simultaneously present in the image.

Let $N$ be a prime number, and $X$ a curve that is intermediate to the cover $X_1(N)\rightarrow X_0(N)$. We study the automorphism group of $X$, and prove that in most cases it is generated by the Galois group of the cover $X\rightarrow X_0(N)$, and any lift of the Atkin–Lehner involution to $X$.