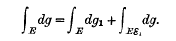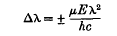Research Article
Concerning some Solutions of the Boundary Layer Equations in Hydrodynamics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-30
-
- Article
- Export citation
A property of continuous arcs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-33
-
- Article
- Export citation
The relation between Riemann's method of summation and Cesàro's
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 34-42
-
- Article
- Export citation
Enumerative Formulae for Surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-71
-
- Article
- Export citation
Representation of the planes of five-dimensional space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 72-81
-
- Article
- Export citation
Some series of squares of Bessel functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 82-87
-
- Article
- Export citation
Note on the Theory of Measure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 88-93
-
- Article
- Export citation
A Geometrical Study of the Hyper-Octohedral Group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 94-98
-
- Article
- Export citation
On the existence of non-combining groups of wave-functions, and on the uniqueness of the solutions of certain wave equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-100
-
- Article
- Export citation
The Thermodynamics of an Elastic Solid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 101-106
-
- Article
- Export citation
On the Equation of State of an Ionised Gas
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-114
-
- Article
- Export citation
Note on Eddy Current Losses in the Sheaths of Rectifier Cables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 115-116
-
- Article
- Export citation
An attempt to detect an Electric Moment in a Light Quantum
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-121
-
- Article
- Export citation
Front matter
PSP volume 26 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 26 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

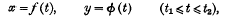
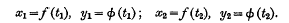
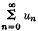 is said to be summable by Riemann's method of order
is said to be summable by Riemann's method of order 
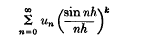
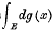 is not continuous there exists a countable set ε
is not continuous there exists a countable set ε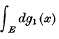 such that
such that