Research Article
On the product of three non-homogeneous linear forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 137-152
-
- Article
- Export citation
On a class of linear integro-differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-163
-
- Article
- Export citation
The gravitational field of a rotating cohesive system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 164-177
-
- Article
- Export citation
Note on the velocity of propagation of gravitation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 178-182
-
- Article
- Export citation
A note on relativistic second quantization
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-195
-
- Article
- Export citation
A note on the Hamiltonian theory of quantization. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 196-204
-
- Article
- Export citation
A note on the theory of dislocation in metals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 205-212
-
- Article
- Export citation
A variational method for determining eigenvalues of the wave equation applied to tropospheric refraction*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-219
-
- Article
- Export citation
A theory of the performance of radar on ship targets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 220-231
-
- Article
- Export citation
The heat of adsorption of diatomic molecules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 232-239
-
- Article
- Export citation
Optical theory of the echelette grating
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 240-253
-
- Article
- Export citation
Demagnetizing coefficients and hysteresis losses of rectangular iron-silicon strips
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 254-261
-
- Article
- Export citation
Note on the structure of liquid helium II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 262-266
-
- Article
- Export citation
The radiations emitted by
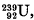 and its formation in the deuteron bombardment of uranium
and its formation in the deuteron bombardment of uranium
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 267-274
-
- Article
- Export citation
Research Notes
On the initial moments of a bounded function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 275-279
-
- Article
- Export citation
Minimum variance and the estimation of several parameters
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 280-283
-
- Article
- Export citation
Geometrical optics and Maxwell's equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 284-286
-
- Article
- Export citation
Stress in an infinite half-plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 287-288
-
- Article
- Export citation
Front matter
PSP volume 43 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 43 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
-
- Article
-
- You have access
- Export citation

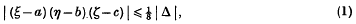

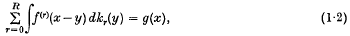
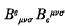 at a point in a plane containing a rotating cohesive system such as a rod is calculated for a point at great distances from the system. It is found that the invariant has a stationary value when the rod is
at a point in a plane containing a rotating cohesive system such as a rod is calculated for a point at great distances from the system. It is found that the invariant has a stationary value when the rod is 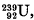 and its formation in the deuteron bombardment of uranium
and its formation in the deuteron bombardment of uranium
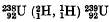 has been studied, and the conclusion reached that the Oppenheimer-Phillips mechanism is responsible for the larger part of the yield.
has been studied, and the conclusion reached that the Oppenheimer-Phillips mechanism is responsible for the larger part of the yield.