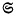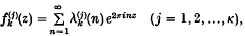Research Article
Reductions of ideals in local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-158
-
- Article
- Export citation
An invariant characterization of pseudo-valuations on a field
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-177
-
- Article
- Export citation
A note on commutators in free products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 178-188
-
- Article
- Export citation
A certain triple Whitehead product
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-197
-
- Article
- Export citation
The dimension of Cartesian product sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 198-202
-
- Article
- Export citation
Lattice coverings with four-dimensional spheres
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 203-208
-
- Article
- Export citation
The inhomogeneous minima of complex cubic norm forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-219
-
- Article
- Export citation
An extension of the Minkowski-Hlawka theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 220-224
-
- Article
- Export citation
Asymptotic formulae in the theory of partitions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 225-241
-
- Article
- Export citation
Tauberian theorems in a Banach lattice, with applications to the LP spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 242-249
-
- Article
- Export citation
Real inequalities with applications to function theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 250-260
-
- Article
- Export citation
An extension of the Ahlfors distortion theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 261-265
-
- Article
- Export citation
The roots of Yn(λη)Jn(λ) – Jn(λη) Yn(λ) = 0
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 266-268
-
- Article
- Export citation
On the computation of oscillatory integrals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 269-277
-
- Article
- Export citation
The concept of order I. The space-time structure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 278-286
-
- Article
- Export citation
The central limit theorem for m-dependent variables asymptotically stationary to second order
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 287-292
-
- Article
- Export citation
A note on Wild's solution of the Boltzmann equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 293-297
-
- Article
- Export citation
Separation of angle variables for helium
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 298-304
-
- Article
- Export citation
The coefficients of certain integral modular forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 305-308
-
- Article
- Export citation
Diffraction by two parallel planes of finite length
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 309-318
-
- Article
- Export citation

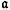 and
and 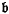 are ideals and
are ideals and 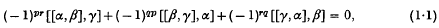
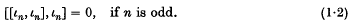

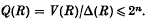

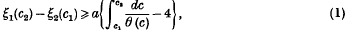

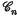 (λ
(λ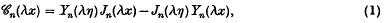
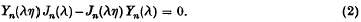
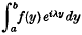 is of frequent occurrence in applied problems. Here λ is real and i is the imaginary unit. Tables of the integrals are often required for a wide range of λ values, some of which may be quite large. Tabulation of the integrand for each λ, followed by ordinary methods of numerical integration, is slow and tedious because the number of points required increases with increasing λ. In this paper formulas are given so that once
is of frequent occurrence in applied problems. Here λ is real and i is the imaginary unit. Tables of the integrals are often required for a wide range of λ values, some of which may be quite large. Tabulation of the integrand for each λ, followed by ordinary methods of numerical integration, is slow and tedious because the number of points required increases with increasing λ. In this paper formulas are given so that once