Research Article
A note on residually finite groups†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 255-256
-
- Article
- Export citation
A note on the homotopy type of PL2
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-258
-
- Article
- Export citation
Massey products in K-theory. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 259-289
-
- Article
- Export citation
On the homotopy-symmetry of sphere bundles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-294
-
- Article
- Export citation
On the differential topology of space-time†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 295-296
-
- Article
- Export citation
Summability methods which include the Riesz typical means. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-300
-
- Article
- Export citation
An extension of Lukacs's result
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-303
-
- Article
- Export citation
Convergence of weighted sums of independent random variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 305-307
-
- Article
- Export citation
A note on sufficient statistics and the exponential family
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 309-313
-
- Article
- Export citation
Quantum mechanics and the gravitational red shift
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-318
-
- Article
- Export citation
On the geodesic completeness of causal space-times
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 319-323
-
- Article
- Export citation
The space-time metric inside a rotating cylinder
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 325-327
-
- Article
- Export citation
Notes on existence of eigenvalues
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 329-332
-
- Article
- Export citation
Slow viscous flow past a rotating sphere
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 333-336
-
- Article
- Export citation
The effects of wall conductivity in magnetohydrodynamic duct flow at high Hartmann numbers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 337-351
-
- Article
- Export citation
On hearing the shape of a drum: further results
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 353-363
-
- Article
- Export citation
Modular spin representations of the symmetric group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-372
-
- Article
- Export citation
Front matter
PSP volume 69 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 69 issue 2 Cover, Back matter and Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b3
-
- Article
-
- You have access
- Export citation

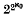
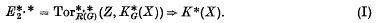


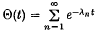 for small positive
for small positive 