Research Article
Local systems and Sylow subgroups in locally finite groups. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-22
-
- Article
- Export citation
A note on a centrality property of finitely generated soluble groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-24
-
- Article
- Export citation
On groups satisfying the converse of Lagrange's theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-32
-
- Article
- Export citation
On groups and 3-manifolds with weak dimension ≤ 1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-35
-
- Article
- Export citation
Completely stretched sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-43
-
- Article
- Export citation
Locally convex topologies and the convex compactness property
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 45-50
-
- Article
- Export citation
Measures vanishing off the symmetric maximal ideals of M(G)†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 51-61
-
- Article
- Export citation
Difference-covers that are not k-sum-covers. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 63-73
-
- Article
- Export citation
An approximate theorem for Borsuk's conjecture
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 75-76
-
- Article
- Export citation
Simultaneous approximation of two additive forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-82
-
- Article
- Export citation
On Riemann summability of functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 83-94
-
- Article
- Export citation
Oscillations of retarded differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-101
-
- Article
- Export citation
Characterizing pure loss GI/G/1 queues with renewal output
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-107
-
- Article
- Export citation
An extension of Lévy's result concerning indecomposability of the Wishart distribution
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-113
-
- Article
- Export citation
Front matter
PSP volume 75 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 75 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

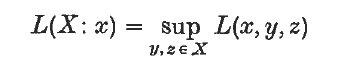
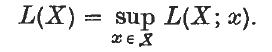
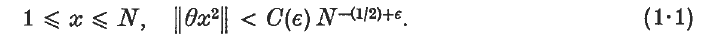


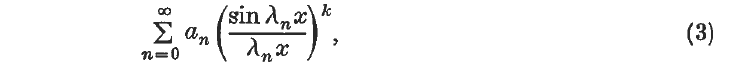

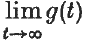 = ∞.
= ∞.