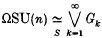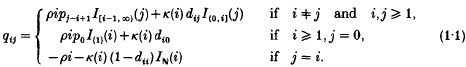Research Article
Groups whose projective characters are Galois conjugate
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 193-197
-
- Article
- Export citation
On a theorem of Birch concerning sums of distinct integers taken from certain sequences
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 199-206
-
- Article
- Export citation
A faithful polynomial representation of Out F3
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 207-213
-
- Article
- Export citation
Equivalences of two-complexes, with applications to NEC-groups
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 215-228
-
- Article
- Export citation
Non-commutative Noetherian Unique Factorization Domains often have stable range one
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 229-235
-
- Article
- Export citation
Flat C(X)-modules and F spaces
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 237-244
-
- Article
- Export citation
Description of most starshaped surfaces
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 245-251
-
- Article
- Export citation
Proving a witness lemma in better-quasiordering theory: the method of ‘extensions’
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 253-262
-
- Article
- Export citation
Splitting ℂP∞ and Bℤ/pn into Thom spectra
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 263-271
-
- Article
- Export citation
The skein polynomial of a planar star product of two links
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 273-276
-
- Article
- Export citation
A Tauberian theorem for statistical convergence
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 277-280
-
- Article
- Export citation
Commutativity of C*-algebras and associativity of JB*-algebras
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 281-291
-
- Article
- Export citation
Twisted crossed products of C*-algebras
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 293-311
-
- Article
- Export citation
Completely positive maps which are compact from L∞ to L1
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 313-323
-
- Article
- Export citation
On Weierstrass-like functions and random recurrent sets
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 325-342
-
- Article
- Export citation
The Brownian bridge as a flat integral
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 343-354
-
- Article
- Export citation
Influence of design on the rate of convergence to normality in L1 regression
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 355-368
-
- Article
- Export citation
The Markov branching process with density-independent catastrophes. II. The subcritical and critical cases
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. 369-383
-
- Article
- Export citation
Front matter
PSP volume 106 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 28 June 2011, pp. f1-f3
-
- Article
-
- You have access
- Export citation