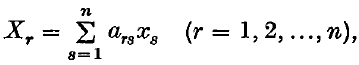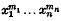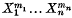Research Article
Two problems on convex bodies
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-7
-
- Article
- Export citation
On covering a regular polygon with a triangle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 8-11
-
- Article
- Export citation
The number of trees with nodes of alternate parity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 12-16
-
- Article
- Export citation
On non-negative forms in real variables some or all of which are non-negative
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 17-25
-
- Article
- Export citation
Inequalities for functions regular in the unit circle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-37
-
- Article
- Export citation
Solutions of certain finite difference equations connected with Laplace's equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 38-51
-
- Article
- Export citation
A method of evaluating the complex zeros of polynomials using polar coordinates
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 52-56
-
- Article
- Export citation
Sequential Monte Carlo
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-78
-
- Article
- Export citation
On queues in which customers are served in random order
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-91
-
- Article
- Export citation
The exact enumeration of self-avoiding walks on a lattice
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 92-101
-
- Article
- Export citation
Applications of Møller's theory on energy and its localization in general relativity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 102-109
-
- Article
- Export citation
The electromagnetic energy and the gravitational mass of a charged particle in general relativity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 110-118
-
- Article
- Export citation
Landau damping for non-Maxwellian distributions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-129
-
- Article
- Export citation
Single-centre expansions for the hydrogen molecular ion. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 130-135
-
- Article
- Export citation
Scattering of plane elastic waves at rough surfaces. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 136-157
-
- Article
- Export citation
Research Notes
On rearrangement of series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 158-159
-
- Article
- Export citation
A short proof of MacMahon's ‘Master Theorem’
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 160
-
- Article
- Export citation
Proofs of some ‘binomial’ identities by means of MacMahon's ‘Master Theorem’
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-162
-
- Article
- Export citation
The effect of queue discipline on waiting time variance
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 163-164
-
- Article
- Export citation
Front matter
PSP volume 58 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f4
-
- Article
-
- You have access
- Export citation

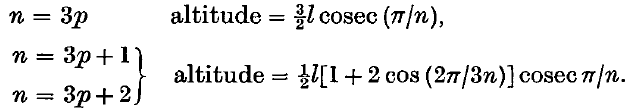
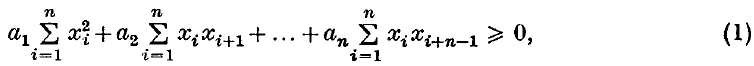


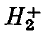 may be obtained using a single-centre expansion, provided that the radial functions are properly determined. In particular, the ground-state energy at the equilibrium internuclear separation of 2 a.u. was found to be within 0·25% of the exact value (Bates, Ledsham and Stewart (2)), and the eigenfunction reproduced all the characteristics of the exact wave-function. The method has now been extended to the odd σ-states, as well as to the two lowest π-states (2
may be obtained using a single-centre expansion, provided that the radial functions are properly determined. In particular, the ground-state energy at the equilibrium internuclear separation of 2 a.u. was found to be within 0·25% of the exact value (Bates, Ledsham and Stewart (2)), and the eigenfunction reproduced all the characteristics of the exact wave-function. The method has now been extended to the odd σ-states, as well as to the two lowest π-states (2 is a rearrangement (in the order of its terms) of the series of complex terms
is a rearrangement (in the order of its terms) of the series of complex terms