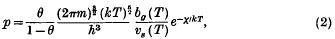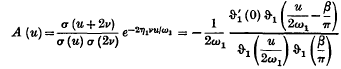Research Article
On the Contacts of Circles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-11
-
- Article
- Export citation
Some Quartic Primals and Associated Cremona Transformations of Four-Dimensional Space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 12-22
-
- Article
- Export citation
The Relations between the Invariants of Two Surfaces in (1, n) Cyclic Correspondence
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-29
-
- Article
- Export citation
Solution of a Moment Problem for Bounded Functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 30-39
-
- Article
- Export citation
The Stability of Viscous Fluid Flow under Pressure between Parallel Planes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 40-54
-
- Article
- Export citation
On the Stability Problem in Hydrodynamics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-66
-
- Article
- Export citation
The Gliding of a Plate on a Stream of Finite Depth. Part II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-85
-
- Article
- Export citation
A Generalization of Picard's Method of Successive Approximation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 86-95
-
- Article
- Export citation
On the Symmetries of the Solutions of a Certain Variational Problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 96-101
-
- Article
- Export citation
On the Linearization of the Energy Density of the Electromagnetic Field
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 102-107
-
- Article
- Export citation
Thermal Properties of an Incompletely Degenerate Fermi Gas
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 108-111
-
- Article
- Export citation
On the Radiation Emitted by a Multipole and its Angular Momentum
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 112-126
-
- Article
- Export citation
The New Action Function and the Unitary Field Theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-137
-
- Article
- Export citation
A Maximum-Minimum Method of Determining the Cardinal Points of a Lens System
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 138-143
-
- Article
- Export citation
Adsorption Isotherms. Critical Conditions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 144-151
-
- Article
- Export citation
The Dissociation Equilibrium of Hydrogen and its Adsorption on Tungsten
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 152-157
-
- Article
- Export citation
On the Annihilation of Positrons
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 158-160
-
- Article
- Export citation
The Errors of Approximation in Jeffreys's Phases
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-178
-
- Article
- Export citation
Experiments on the Efficiencies of Production and the Half-Lives of Radio-Carbon and Radio-Nitrogen
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-182
-
- Article
- Export citation
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 183
-
- Article
-
- You have access
- Export citation




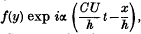 , it is found that, for small Reynolds numbers
, it is found that, for small Reynolds numbers 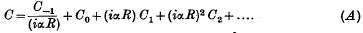
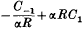 in this approximation, is found to be positive. When α is of the order of unity, the value of
in this approximation, is found to be positive. When α is of the order of unity, the value of  of the first is about 50 for the symmetrical disturbance and 100 for the antisymmetrical disturbance.
of the first is about 50 for the symmetrical disturbance and 100 for the antisymmetrical disturbance. 
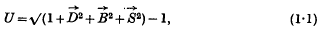
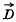 is the electric displacement,
is the electric displacement, 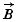 the magnetic induction,
the magnetic induction, 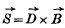 the Poynting vector) with the help of the commutation laws for these vectors.
the Poynting vector) with the help of the commutation laws for these vectors.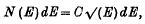
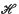 as an action function. This new form of the variational principle enables us to find a new special action function, which conserves the chief features of Born's theory while changing some of its former results. To a given charge correspond two static solutions with central symmetry, one giving a finite, the other an infinite energy. The potential of the one (light) particle is analogous to that in Born's theory while the potential of the other resembles a potential barrier. Also, by using the new action function, the symmetry between electric and magnetic fields ceases to exist.
as an action function. This new form of the variational principle enables us to find a new special action function, which conserves the chief features of Born's theory while changing some of its former results. To a given charge correspond two static solutions with central symmetry, one giving a finite, the other an infinite energy. The potential of the one (light) particle is analogous to that in Born's theory while the potential of the other resembles a potential barrier. Also, by using the new action function, the symmetry between electric and magnetic fields ceases to exist.