Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T14:17:57.414Z Has data issue: false hasContentIssue false
  • English
  • Français

Zur Summabilitätstheorie der Fourierschen Doppelreihe

Published online by Cambridge University Press:  24 October 2008

Géza Grünwald
Géza Grünwald
Affiliation:
Tungsram Research LaboratoryUjpest 4Near Budapest
Get access Rights & Permissions [Opens in a new window]

Extract

Es sei f(ξ) eine L-integrierbare und nach 2π periodische Funktion der reellen Variabeln ξ und es sei {sn} die Folge der Partialsummen ihrer Fourierschen Reihe an einer Stelle ξ = x, wo die Funktion stetig ist. Dann ist nach einem klassischen Satze von Fejér

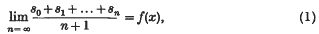
und nach Hardy und Littlewood

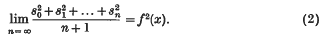
Vor kurzem hat L. Fejér gefunden, dass der Hardy-Littlewoodsche Satz (2) Spezialfall eines “gewöhnlichen” Summabilitätssatzes wie (1) ist, der sich aber auf die Fouriersche Reihe einer Funktion zweier Variabeln bezieht. Dieser Satz ist der folgende.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 35 , Issue 3 , July 1939 , pp. 343 - 350
Copyright
Copyright © Cambridge Philosophical Society 1939

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Fejér, L., “Sur les fonctions bornées et intégrables”, C.R. Acad. Sci., Paris, 131 (1900), 984.Google Scholar

† Hardy, G. H. et Littlewood, J. E., “Sur la série de Fourier d'une fonction à carré sommable”, C.R. Acad. Sci., Paris, 156 (1913), 1307.Google Scholar

‡ Fejér, L., “Zur Summabilitätstheorie der Fourierschen und Laplaceschen Reihe”, Proc. Cambridge Phil. Soc. 34 (1938), 503.CrossRefGoogle Scholar

* In der ursprünglichen Fassung dieses Satzes hatte ich vorausgesetzt, dass die Funktion überall stetig ist. Die wichtige Bemerkung, dass schon die lokale Stetigkeit hinreichend ist, verdanke ich einer freundlichen Mitteilung von Herrn Prof. W. Rogosinski. Der § 4 stammt von W. Rogosinski.

† Zygmund, Siehe z.B., Trigonometrical series (Warsaw, 1935), S. 238.Google Scholar