Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T12:56:49.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Wiener amalgams, Hardy spaces and summability of Fourier series

Published online by Cambridge University Press:  01 September 2008

FERENC WEISZ
FERENC WEISZ*
Affiliation:
Department of Numerical Analysis, Eötvös L. University, Pázmány P. sétány 1/C., H-1117 Budapest, Hungary. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A general summability method, the so called θ-summability is considered for multi-dimensional Fourier series, where θ is in the Wiener algebra W(C,ℓ1)(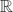d). It is based on the use of Wiener amalgam spaces, weighted Feichtinger's algebra, Herz and Hardy spaces. Under some conditions on θ, it is proved that the maximal operator of the θ-means is bounded from the Hp Hardy space to Lp (or Hp). This implies some norm and almost everywhere convergence results for the θ-means. Large number of special cases of the θ-summation are considered.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 145 , Issue 2 , September 2008 , pp. 419 - 442
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]II, A. Baernstein and Sawyer, E. T.. Embedding and multiplier theorems for H p(Rn). Number 318 in Mem. Amer. Math. Soc. (1985).CrossRefGoogle Scholar
[2]Berens, H., Li, Z. and Xu, Y.. On l-1 Riesz summability of the inverse Fourier integral. Indag. Mathem. 12 (2001), 41–53.CrossRefGoogle Scholar
[3]Berens, H. and Xu, Y.. l-1 summability of multiple Fourier integrals and positivity. Math. Proc. Camb. Phil. Soc. 122 (1997), 149–172.CrossRefGoogle Scholar
[4]Bergh, J. and Löfström, J.. Interpolation Spaces, an Introduction (Springer, 1976).Google Scholar
[5]Bokor, J. and Schipp, F.. Approximate identification in Laguerre and Kautz bases. Automatica 34 (1998), 463–468.CrossRefGoogle Scholar
[6]Butzer, P. L. and Nessel, R. J.. Fourier Analysis and Approximation (Birkhäuser Verlag 1971).CrossRefGoogle Scholar
[7]Davis, K. M. and Chang, Y.-C.. Lectures on Bochner-Riesz Means. volume 114 of London Mathematical Society Lecture Note Series (Cambridge University Press, 1987).Google Scholar
[8]Feichtinger, H. G.. On a new Segal algebra. Monatsh. Math. 92 (1981), 269–289.CrossRefGoogle Scholar
[9]Feichtinger, H. G.. Minimal Banach spaces and atomic representations. Publ. Math. Debrecen 34 (1987), 231–240.CrossRefGoogle Scholar
[10]Feichtinger, H. G.. An elementary approach to Wiener's third Tauberian theorem for the Euclidean n-space. In Symposia Math., volume XXIX of Analisa Armonica (Cortona, 1988), pages 267–301.Google Scholar
[11]Feichtinger, H. G.. Atomic characterizations of modulation spaces through Gabor-type representations. In Proc. Conf. Constructive Function Theory, Edmonton, July 1986. Rocky Mount. J. Math. 19 (1989), pages 113–126.Google Scholar
[12]Feichtinger, H. G. and Weisz, F.. The Segal algebra bS0(Rd) and norm summability of Fourier series and Fourier transforms. Monatsh. Math. 148 (2006), 333–349.CrossRefGoogle Scholar
[13]Feichtinger, H. G. and Weisz, F.. Wiener amalgams and pointwise summability of Fourier transforms and Fourier series. Math. Proc. Camb. Phil. Soc. 140 (2006), 509–536.Google Scholar
[14]Feichtinger, H. G. and Zimmermann, G.. A Banach space of test functions for Gabor analysis. In Feichtinger, H. G. and Strohmer, T., editors, Gabor Analysis and Algorithms. Theory and Applications. Applied and Numerical Harmonic Analysis (Birkhäuser, 1998), pages 123–170.Google Scholar
[15]Garcia–Cuerva, J.. Hardy spaces and Beurling algebras. J. London Math. Soc. 39 (1989), 499–513.CrossRefGoogle Scholar
[16]Garcia-Cuerva, J. and Herrero, M.-J. L.. A theory of Hardy spaces associated to the Herz spaces. Proc. London Math. Soc. 69 (1994), 605–628.CrossRefGoogle Scholar
[17]Grafakos, L.. Classical and Modern Fourier Analysis (Pearson Education, 2004).Google Scholar
[18]Grafakos, L., Li, X. and Yang, D.. Bilinear operators on Herz-type Hardy spaces. Trans. Amer. Math. Soc. 350 (1998), 1249–1275.CrossRefGoogle Scholar
[20]Gröchenig, K.. Foundations of Time-Frequency Analysis (Birkhäuser, 2001).CrossRefGoogle Scholar
[20]Gröchenig, K. and Heil, C.. Gabor meets Littlewood–Paley: Gabor expansions in L p(Rd). Studia Math. 146 (2001), 15–33.CrossRefGoogle Scholar
[21]Heil, C.. An introduction to weighted Wiener amalgams. In Krishna, M., Radha, R., and Thangavelu, S., editors, Wavelets and their Applications (Allied Publishers Private Limited, 2003), pages 183–216.Google Scholar
[22]Herz, C.. Lipschitz spaces and Bernstein's theorem on absolutely convergent Fourier transforms. J. Math. Mech. 18 (1968), 283–324.Google Scholar
[23]Komori, Y.. Notes on commutators on Herz-type spaces. Arch. Math. 81 (2003), 318–326.CrossRefGoogle Scholar
[24]Komori, Y.. Weak type estimates for Calder'on–Zygmund operators on Herz spaces at critical indexes. Math. Nachr. 259 (2003), 42–50. CrossRefGoogle Scholar
[25]Li, X. and Yang, D.. Boundedness of some sublinear operators on Herz spaces. Illinois J. Math. 40 (1996), 484–501.CrossRefGoogle Scholar
[26]Lu, S.. Four Lectures on Real Hp Spaces (World Scientific, 1995).CrossRefGoogle Scholar
[27]Natanson, G. M. and Zuk, V. V.. Trigonometric Fourier Series and Elements of Approximation Theory (Leningrad. University, 1983) (in Russian).Google Scholar
[28]Schipp, F. and Bokor, J.. L∞ system approximation algorithms generated by φ summations. Automatica 33 (1997), 2019–2024.CrossRefGoogle Scholar
[29]Stein, E. M.. Harmonic Analysis: Real-variable Methods, Orthogonality and Oscillatory Integrals (Princeton University Press, 1993).Google Scholar
[30]Stein, E. M. and Weiss, G.. Introduction to Fourier Analysis on Euclidean Spaces (Princeton University Press, 1971).Google Scholar
[31]Szili, L.. On the summability of trigonometric interpolation processes. Acta Math. Hungar. 91 (2001), 131–158.CrossRefGoogle Scholar
[32]Szili, L. and Vértesi, P.. On uniform convergence of sequences of certain linear operators. Acta Math. Hungar. 91 (2001), 159–186.CrossRefGoogle Scholar
[33]Torchinsky, A.. Real-variable Methods in Harmonic Analysis (Academic Press, 1986).Google Scholar
[34]Trigub, R. M. and Belinsky, E. S.. Fourier Analysis and Approximation of Functions (Kluwer Academic Publishers, 2004).CrossRefGoogle Scholar
[35]Walnut, D.. Continuity properties of the Gabor frame operator. J. Math. Anal. Appl. 165 (2) (1992), 479–504.CrossRefGoogle Scholar
[36]Weisz, F.. Cesàro summability of one- and two-dimensional trigonometric-Fourier series. Colloq. Math. 74 (1997), 123–133.CrossRefGoogle Scholar
[37]Weisz, F.. θ-summation and Hardy spaces. J. Appr. Theory 107 (2000), 121–142.CrossRefGoogle Scholar
[38]Weisz, F.. Several dimensional θ-summability and Hardy spaces. Math. Nachr. 230 (2001), 159–180.3.0.CO;2-L>CrossRefGoogle Scholar
[39]Weisz, F.. Summability of Multi-dimensional Fourier Series and Hardy Spaces. Mathematics and Its Applications (Kluwer Academic Publishers, 2002).CrossRefGoogle Scholar
[40]Weisz, F.. θ-summability of Fourier series. Acta Math. Hungar. 103 (2004), 139–176.CrossRefGoogle Scholar
[41]Zhizhiashvili, L.. Trigonometric Fourier Series and their Conjugates (Kluwer Academic Publishers 1996).CrossRefGoogle Scholar
[42]Zygmund, A.. Trigonometric Series (Cambridge Press, 2002).Google Scholar