Article contents
Whitney equisingularity of families of surfaces in ℂ3
Published online by Cambridge University Press: 15 January 2018
Abstract
In this paper, we study families of singular surfaces in ℂ3 parametrised by 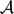 $\mathcal {A}$-finitely determined map germs. We consider the topological triviality and Whitney equisingularity of an unfolding F of a finitely determined map germ f : (ℂ2, 0) → (ℂ3, 0). We investigate the following question: topological triviality implies Whitney equisingularity of the unfolding F? We provide a complete answer to this question, by giving counterexamples showing how the conjecture can be false.
$\mathcal {A}$-finitely determined map germs. We consider the topological triviality and Whitney equisingularity of an unfolding F of a finitely determined map germ f : (ℂ2, 0) → (ℂ3, 0). We investigate the following question: topological triviality implies Whitney equisingularity of the unfolding F? We provide a complete answer to this question, by giving counterexamples showing how the conjecture can be false.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 166 , Issue 2 , March 2019 , pp. 353 - 369
- Copyright
- Copyright © Cambridge Philosophical Society 2018
References
REFERENCES
- 6
- Cited by


