Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T19:14:57.644Z Has data issue: false hasContentIssue false
  • English
  • Français

When rings of differential operators are maximal orders

Published online by Cambridge University Press:  24 October 2008

M. Chamarie  and
J. T. Stafford
M. Chamarie
Affiliation:
Département de Mathematiques, Université Claude Bernard, Lyon, France
J. T. Stafford
Affiliation:
Department of Pure Mathematics, University of Leeds, Leeds LS2 9JT
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be a commutative domain, finitely generated as an algebra over a field k of characteristic zero and write 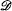(A) for the ring of k -linear differential operators. Then 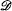A is an Ore domain with quotient division ring, say Q. Our main result is that 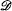A is a maximal order in Q if and only if (i) A = ∩{Ap: height (p) = 1} and (ii) A is geometrically unibranched. In this case 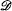A is also a Krull domain with no reflexive ideals. We also determine some conditions under which 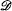A is simple.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 399 - 410
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bass, H.. Finitistic dimension and a homological generalisation of semiprimary rings. Trans. Amer. Math. Soc. 95 (1960), 466–488.CrossRefGoogle Scholar
[2]Bernstein, J. N., Gelfand, I. M. and Gelfand, S. I.. Differential operators on the cubic cone. Russian Math. Surveys 27 (1972), 169–174.CrossRefGoogle Scholar
[3]Bjork, J. E.. Rings of Differential Operators (North Holland, 1979).Google Scholar
[4]Bourbaki, N.. Commutative Algebra (Hermann, 1972).Google Scholar
[5]Chamarie, M.. Anneaux de Krull non commutatifs. J. Algebra 72 (1981), 210–222.CrossRefGoogle Scholar
[6]Chamarie, M.. Modules sur les anneaux de Krull non commutatifs. In Séminaire d'Algèbre P. Dubreil et M.-P. Malliavin, Lecture Notes in Math., vol. 1029 (Springer-Verlag, 1983), 283–310.CrossRefGoogle Scholar
[7]Ferrand, D.. Monomorphismes et morphismes absolument plats. Bull. Soc. Math. France 100 (1972), 97–128.CrossRefGoogle Scholar
[8]Hart, R.. Differential operators on affine algebras. J. London Math. Soc. 28 (1983), 470–476.CrossRefGoogle Scholar
[9]Hart, R. and Smith, S. P.. Differential operators on some singular surfaces. Bull. London Math. Soc. 19 (1987), 145–148.CrossRefGoogle Scholar
[10]Humphreys, J. E.. Linear Algebraic Groups (Springer-Verlag, 1981).Google Scholar
[11]Ishibashi, Y.. Remarks on a conjecture of Nakai. J. Algebra 95 (1985), 31–45.Google Scholar
[12]Levasseur, T.. Anneaux d'operateurs différentiels. In Séminaire d'Algèbre P. Dubreil et M.-P. Malliavin, Lecture Notes in Math., vol. 867 (Springer-Verlag, 1981), 157–173.CrossRefGoogle Scholar
[13]Matsumura, H.. Commutative Algebra (W. A. Benjamin, 1970).Google Scholar
[14]McConnell, J. C. and Robson, J. C.. Non-commutative Noetherian Rings (J. Wiley, to appear).Google Scholar
[15]Muhasky, J. L.. The differential operator rings on an affine curve. Trans. Amer. Math. Soc. (to appear).Google Scholar
[16]Smith, S. P.. Curves, differential operators and finite dimensional algebras. In Séminaire d'Algèbre P. Dubreil et M.-P. Malliavin, Lecture Notes in Math. (Springer-Verlag, to appear).Google Scholar
[17]Smith, S. P. and Stafford, J. T.. Differential operators on an affine curve. Proc. London Math. Soc. (to appear).Google Scholar
[18]Stafford, J. T.. Modules over prime Krull rings. J. Algebra 95 (1985), 332–342.CrossRefGoogle Scholar
[19]Stafford, J. T.. Module structure of Weyl algebras. J. London Math. Soc. 18 (1978), 429–442.CrossRefGoogle Scholar
[20]Sweedler, M. E.. Groups of simple algebras. Publ. Math. IHES 45 (1975), 79–189.Google Scholar
[21]Van Doorn, M. G. M. and Van Den Essen, A. R. P.. Dn -modules with support on a curve. To appear.Google Scholar