Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rychlik, E.
and
Rychlik, Z.
1980.
Probability Theory on Vector Spaces II.
Vol. 828,
Issue. ,
p.
244.
Csörgó, M.
and
Rychlik, Z.
1981.
Asymptotic properties of randomly indexed sequences of random variables.
Canadian Journal of Statistics,
Vol. 9,
Issue. 1,
p.
101.
Butzer, Paul L.
and
Schulz, Dietmar
1984.
Limit Theorems with ϑ-Rates for Random Sums of Dependent Banach-Valued Random Variables.
Mathematische Nachrichten,
Vol. 119,
Issue. 1,
p.
59.
Rychlik, Eugeniusz
1984.
Probability Theory on Vector Spaces III.
Vol. 1080,
Issue. ,
p.
244.
Siegel, G.
1988.
Convergence of Randomly Selected Sums in a Separable Banach Space.
Mathematische Nachrichten,
Vol. 139,
Issue. 1,
p.
139.
Krajka, A.
and
Rychlik, Z.
1988.
The order of approximation in the central limit theorem for random summation.
Acta Mathematica Hungarica,
Vol. 51,
Issue. 1-2,
p.
109.
Kowalski, Piotr
and
Rychlik, Zdzisŀaw
1998.
Asymptotic Methods in Probability and Statistics.
p.
13.
Becker-Kern, P.
2004.
Random Sums of Independent Random Vectors Attracted by (Semi)-Stable Hemigroups.
Journal of Applied Analysis,
Vol. 10,
Issue. 1,
Gut, Allan
and
Stadtmüller, Ulrich
2013.
Records in subsets of a random field.
Statistics & Probability Letters,
Vol. 83,
Issue. 3,
p.
689.
Logachov, Artem V.
and
Mogulskii, Anatolii A.
2018.
Anscombe-type theorem and moderate deviations for trajectories of a compound renewal process.
Journal of Mathematical Sciences,
Vol. 229,
Issue. 1,
p.
36.


 . Let {
. Let {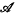 ,
, 