Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T17:24:26.679Z Has data issue: false hasContentIssue false
  • English
  • Français

Vector bundles that fill n-space

Published online by Cambridge University Press:  24 October 2008

S. A. Robertson  and
R. L. E. Schwarzenberger
S. A. Robertson
Affiliation:
University of Liverpool and University of Warwick
R. L. E. Schwarzenberger
Affiliation:
University of Liverpool and University of Warwick
Get access Rights & Permissions [Opens in a new window]

Extract

The idea of exact filling bundle may be described roughly as follows. Suppose that ξk is a vector bundle with fibre Rk, total space E(ξk) and base X. We say that ξk is a real k-plane bundle on X. Let in be the trivial n-plane bundle on X so that E(in) = X × Rn. A bundle monomorphism j: ξk → in defines a map 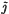: E(ξk)→Rn obtained by composition of the embedding E(ξk)→E(in) and the product projection E(in) → Rn. The map 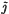represents each fibre of ξk as a k-plane in Rn.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 61 , Issue 4 , October 1965 , pp. 869 - 875
Copyright
Copyright © Cambridge Philosophical Society 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1) Borel, A. and Hirzebruch, F. Characteristic classes and homogeneous spaces I, II. American J. Math. 80 (1958), 458–538 and 81 (1959), 315–382.CrossRefGoogle Scholar
(2) Bott, R. The space of loops on a Lie group. Michigan Math. J. 5 (1958), 35–61.CrossRefGoogle Scholar
(3) Grothendieck, A. La théorie des classes de Chern. Bull. Soc. Math. France, 86 (1958), 137–154.Google Scholar
(4) Hopf, H. Zur Topologie der Abbildungen von Mannigfaltigkeiten I, II. Math. Ann. 100 (1928), 579–608 and 102 (1930), 562–623.CrossRefGoogle Scholar
(5) Massey, W. S. On the Stiefel-Whitney classes of a manifold. American J. Math. 82 (1960), 92–102.CrossRefGoogle Scholar
(6) Milnor, J. Differential topology. Lecture notes by Munkres, J.. Princeton University, 1958.Google Scholar
(7) Milnor, J. Some consequences of a theorem of Bott. Ann. Math. 68 (1958), 444–449.CrossRefGoogle Scholar
(8) Robertson, S. A. On filling n-space with r-planes. J. London Math. Soc. 36 (1961), 111–121.CrossRefGoogle Scholar
(9) Robertson, S. A. Certain homeomorphs of real projective spaces. J. London Math. Soc. 37 (1962), 249–251.CrossRefGoogle Scholar
(10) Robertson, S. A. Generalised constant width for manifolds. Michigan Math. J. 11 (1964), 97–105.CrossRefGoogle Scholar
(11) Robertson, S. A. On transnormal manifolds. (To appear.)Google Scholar
(12) Schwarzenberger, R. L. E. Vector bundles on the projective plane. Proc. London Math. Soc. 11 (1961), 623–640.CrossRefGoogle Scholar
(13) Schwarzenberger, R. L. E. The secant bundle of a projective variety. Proc. London Math. Soc. 14 (1964), 369–384.CrossRefGoogle Scholar