Variation of the algebraic λ-invariant over a solvable extension

Abstract

Fix an odd prime p. Let 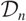$\mathcal{D}_n$ denote a non-abelian extension of a number field K such that 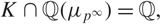$K\cap\mathbb{Q}(\mu_{p^{\infty}})=\mathbb{Q}, $ and whose Galois group has the form 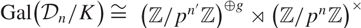$ \text{Gal}\big(\mathcal{D}_n/K\big)\cong \big(\mathbb{Z}/p^{n'}\mathbb{Z}\big)^{\oplus g}\rtimes \big(\mathbb{Z}/p^n\mathbb{Z}\big)^{\times}\ $ where g > 0 and 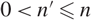$0 \lt n'\leq n$. Given a modular Galois representation 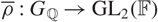$\overline{\rho}:G_{\mathbb{Q}}\rightarrow \text{GL}_2(\mathbb{F})$ which is p-ordinary and also p-distinguished, we shall write 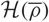$\mathcal{H}(\overline{\rho})$ for the associated Hida family. Using Greenberg’s notion of Selmer atoms, we prove an exact formula for the algebraic λ-invariant

\begin{equation} \lambda^{\text{alg}}_{\mathcal{D}_n}(f) \;=\; \text{the number of zeroes of } \text{char}_{\Lambda}\big(\text{Sel}_{\mathcal{D}_n^{\text{cy}}}\big(f\big)^{\wedge}\big) \end{equation}

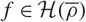at all $f\in\mathcal{H}(\overline{\rho})$, under the assumption 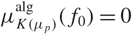$\mu^{\text{alg}}_{K(\mu_p)}(f_0)=0$ for at least one form f₀. We can then easily deduce that 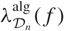$\lambda^{\text{alg}}_{\mathcal{D}_n}(f)$ is constant along branches of 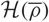$\mathcal{H}(\overline{\rho})$, generalising a theorem of Emerton, Pollack and Weston for 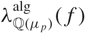$\lambda^{\text{alg}}_{\mathbb{Q}(\mu_{p})}(f)$.

For example, if 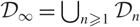$\mathcal{D}_{\infty}=\bigcup_{n\geq 1}\mathcal{D}_n$ has the structure of a p-adic Lie extension then our formulae include the cases where: either (i) 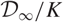$\mathcal{D}_{\infty}/K$ is a g-fold false Tate tower, or (ii) 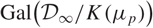$\text{Gal}\big(\mathcal{D}_{\infty}/K(\mu_p)\big)$ has dimension ≤ 3 and is a pro-p-group.