Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-09T04:07:15.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform perfectness of the Berkovich Julia sets in non-archimedean dynamics

Part of: Arithmetic and non-Archimedean dynamical systems Other generalizations Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  21 December 2021

YÛSUKE OKUYAMA
YÛSUKE OKUYAMA*
Affiliation:
Division of Mathematics, Kyoto Institute of Technology, Sakyo-ku, Kyoto 606-8585, Japan. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that a rational function f of degree 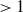$>1$ on the projective line over an algebraically closed field that is complete with respect to a non-trivial and non-archimedean absolute value has no potentially good reductions if and only if the Berkovich Julia set of f is uniformly perfect. As an application, a uniform regularity of the boundary of each Berkovich Fatou component of f is also established.

MSC classification

Primary: 37P50: Dynamical systems on Berkovich spaces
Secondary: 11S82: Non-Archimedean dynamical systems 31C15: Potentials and capacities
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 3 , November 2022 , pp. 573 - 590
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, M. and Rumely, R. Potential theory and dynamics on the Berkovich projective line, Vol. 159 of Mathematical Surveys and Monographs, American Mathematical Society, Providence, RI (2010).CrossRefGoogle Scholar
Benedetto, R. L. Dynamics in one non-archimedean variable, Vol. 198 of Graduate Studies in Mathematics, American Mathematical Society, Providence, RI (2019).Google Scholar
Berkovich, V. G. Spectral theory and analytic geometry over non-Archimedean fields, Vol. 33 of Mathematical Surveys and Monographs, American Mathematical Society, Providence, RI (1990).Google Scholar
Eremenko, A. Julia sets are uniformly perfect (1992), manuscript.Google Scholar
Favre, C. and Jonsson, M. The valuative tree, Vol. 1853 of Lecture Notes in Mathematics, Springer-Verlag, Berlin (2004).CrossRefGoogle Scholar
Favre, C., Kiwi, J. and Trucco, E. A non-Archimedean Montel’s theorem, Compos. Math., 148, 3 (2012), 966–990.CrossRefGoogle Scholar
Favre, C. and Rivera-Letelier, J. Équidistribution quantitative des points de petite hauteur sur la droite projective, Math. Ann., 335, 2 (2006), 311–361.CrossRefGoogle Scholar
Hinkkanen, A. Julia sets of rational functions are uniformly perfect, Math. Proc. Cambridge Philos. Soc., 113, 3 (1993), 543–559.Google Scholar
Hsia, L.-C. Closure of periodic points over a non-Archimedean field, J. London Math. Soc. (2), 62, 3 (2000), 685–700.CrossRefGoogle Scholar
Jonsson, M. Dynamics on Berkovich spaces in low dimensions, Berkovich Spaces and Applications, Vol. 2119 of Lecture Notes in Mathematics, Springer, Cham (2015), 205–366.Google Scholar
Kawaguchi, S. and Silverman, J. H. Nonarchimedean Green functions and dynamics on projective space, Math. Z., 262, 1 (2009), 173–197.CrossRefGoogle Scholar
Lithner, J. Comparing two versions of Markov’s inequality on compact sets, J. Approx. Theory, 77, 2 (1994), 202–211.CrossRefGoogle Scholar
Mañé, R. and da Rocha, L. F. Julia sets are uniformly perfect, Proc. Amer. Math. Soc., 116, 3 (1992), 251–257.Google Scholar
Okuyama, Y. Effective divisors on the projective line having small diagonals and small heights and their application to adelic dynamics, Pacific J. Math., 280, 1 (2016), 141–175.CrossRefGoogle Scholar
Okuyama, Y. and Stawiska, M. On a characterization of polynomials among rational functions in non-archimedean dynamics, Arnold Math. J., 6, 3-4 (2020), 407–430.CrossRefGoogle Scholar
Pommerenke, C. Uniformly perfect sets and the Poincaré metric, Ark. Math., 32 (1979), 192–199.CrossRefGoogle Scholar
Rodrguez Vízquez, R. Non-archimedean normal families, arXiv e-prints (Jul. 2016), arXiv:1607.05976.Google Scholar
Rumely, R. and Winburn, S. The Lipschitz Constant of a Nonarchimedean Rational Function, arXiv e-prints (Dec. 2015), arXiv:1512.01136.Google Scholar
Siciak, J. Wiener’s type regularity criteria on the complex plane, Ann. Polon. Math., 66 (1997), 203–221, Volume dedicated to the memory of Włodzimierz Mlak.CrossRefGoogle Scholar
Sugawa, T. Uniformly perfect sets: analytic and geometric aspects [translation of Sügaku 53 (2001), no. 4, 387–402; MR1869018], Vol. 16 (2003), 225–242, Sugaku Expositions.Google Scholar
Thuillier, A. Théorie du potentiel sur les courbes en géométrie analytique non archimédienne. Applications à la théorie d’Arakelov, PhD thesis, Université Rennes 1 (2005).Google Scholar