Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-04T10:37:51.743Z Has data issue: false hasContentIssue false
  • English
  • Français

Triviality of the ℓ-class groups in 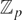$\mathbb{Z}_{p}$-extensions of 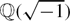$\mathbb{Q}(\sqrt{-1})$ for split primes p ≡ 1 modulo 4

Published online by Cambridge University Press:  12 May 2014

JACK LAMPLUGH
JACK LAMPLUGH*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridge, CB3 0WA. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the class numbers in the finite layers of certain non-cyclotomic 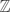$\mathbb{Z}$p-extensions of the imaginary quadratic field 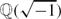$\mathbb{Q}(\sqrt{-1})$, for all primes p ≡ 1 modulo 4. By studying the Mahler measure of elliptic units, we are able to show that there are only finitely many primes ℓ congruent to a primitive root modulo p2 that divide any of the class numbers in the $\mathbb{Z}$p-extension.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 157 , Issue 1 , July 2014 , pp. 169 - 188
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bauer, H.Numeriche bestimmung von Klassenzahlen reeller zyklischer zahlkörper. J. Number Theory 1 (1969), 161–162.Google Scholar
[2]Coates, J.Elliptic curves with complex multiplication and Iwasawa theory. Bull. London Math. Soc. 23 (1991), 321–350.Google Scholar
[3]Coates, J. and Sujatha, R. Cyclotomic fields and zeta values. Springer Monogr. Math. (2006).Google Scholar
[4]Coates, J. and Wiles, A.On p-adic L-functions and elliptic units. J. Austral. Math. Soc. Ser. A 26 (1978), 1–25.Google Scholar
[5]Cohn, H.A numerical study of Weber's real class number calculation I. Numer. Math. 2 (1960), 347–362.Google Scholar
[6]de Shalit, E.The Iwasawa theory of elliptic curves with complex multiplication. Perspect. Math. vol. 3 (1987).Google Scholar
[7]Fukuda, T. and Komatsu, K.Weber's class number problem in the cyclotomic $\mathbb{Z}$2-extension of $\mathbb{Q}$, III. Int. J. Number Theory 7 (6) (2011) 1627–1635.Google Scholar
[8]Goldstein, C. and Schappacher, N.Séries d'Eisenstein et fonctions L de courbes elliptiques à multiplication complexe. J. Reine Angew. Math. 327 (1981), 184–218.Google Scholar
[9]Horie, K.Ideal class groups of Iwasawa-theoretical abelian extensions over the rational field. J. London Math. Soc. 66 (2002), 257–275.CrossRefGoogle Scholar
[10]Horie, K. and Horie, M.The narrow class groups of some $\mathbb{Z}$p-extensions over the rationals. Acta Arith. 135 (2) (2008), 159–180.Google Scholar
[11]Horie, K. and Horie, M.The ideal class group of the $\mathbb{Z}$23-extension over the rational field. Abh. Math. Semin. Univ. Hambg. 80 (1) (2010), 47–57.Google Scholar
[12]Jensen, J. L. V. W.Sur un nouvel et important thorme de la theorie des fonctions. Acta Math. 22 (1899), 359–364.CrossRefGoogle Scholar
[13]Lamplugh, J. An analogue of the Washington–Sinnott theorem for elliptic curves with complex multiplication I, to appear.Google Scholar
[14]Lamplugh, J. An analogue of the Washington–Sinnott theorem for elliptic curves with complex multiplication II, to appear.Google Scholar
[15]Lang, S.Algebraic Number Theory, 2nd edition, Grad. Texts in Math., vol. 110, (Springer-Verlag, New York, Heidelberg, Berlin, 1994).Google Scholar
[16]Mahler, K.On some inequalities for polynomials in several variables. J. London Math. Soc. 37 (1962), 341–344.Google Scholar
[17]Masley, J.Class numbers of real cyclic number fields with small conductor. Compositio Math. 37 (1978), 297–319.Google Scholar
[18]Miller, J. Class numbers of totally real fields and applications to the Weber class number problem, preprint. http://www.math.rutgers.edu/~jcmiller/ClassNumbersAndWeberProblem.pdf.Google Scholar
[19]Morisawa, T.Mahler measure of the Horie unit and Weber's class number problem in the cyclotomic $\mathbb{Z}$3-extension of $\mathbb{Q}$. Acta Arith. 153 (2012) 35–49.CrossRefGoogle Scholar
[20]Morisawa, T. and Okazaki, R. Mahler measure and Weber's class number problem in the cyclotomic $\mathbb{Z}$p-extension of $\mathbb{Q}$ for prime numbers p. Tohoku Math. J., in press.Google Scholar
[21]Robert, G.Unités elliptiques et formules pour le nombre de classes des extensions abéliennes d'un corps quadratique imaginaire. Mém. Soci. Math. France. 36 (1973), 5–77.Google Scholar
[22]Silverman, J.The Arithmetic of Elliptic Curves. Grad. Texts in Math. 106 (Springer-Verlag, 1986).Google Scholar
[23]van der Linden, F.Class number computations of real abelian number fields. Math. Comp. 39 (1982), 693–707.Google Scholar
[24]Washington, L.The non-p-part of the class number in a cyclotomic $\mathbb{Z}$p-extension. Invent. Math. 49 (1978), 87–97.Google Scholar
[25]Weber, H.Theorie der abelschen zahlkörper. Acta. Math. 8 (1886), 193–263.CrossRefGoogle Scholar