Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T17:13:48.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient Oscillations in a Loud-Speaker Horn

Published online by Cambridge University Press:  24 October 2008

N. W. McLachlan  and
A. T. Mckay
Get access Rights & Permissions [Opens in a new window]

Extract

The steady state theory of sound propagation in exponential loud-speaker horns is well known. The problem of transients, however, has not been treated hitherto, so in this paper it is proposed to consider what happens when the air particles at the throat of the horn are suddenly set in motion. To avoid difficulties which arise in treating sound propagation in the horn when the linear dimensions of the cross-section are comparable with the wave-length of the sound, the following

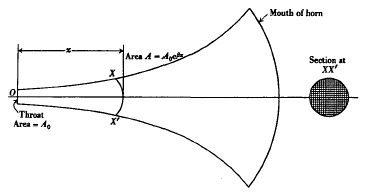
artifice is postulated. The axis of the horn is linear and the air column is divided up into a large number of frictionless conduits by very thin rigid partitions as indicated in Fig. 1. The cross-section of each conduit expands exponentially from the throat towards the mouth of the horn. The major linear dimension of the section of a conduit at the mouth is small in comparison with the wave-length of the highest frequency to be reproduced.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 32 , Issue 2 , May 1936 , pp. 265 - 275
Copyright
Copyright © Cambridge Philosophical Society 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* This means the highest frequency in the range covered by the horn. In general the range 40 to 10,000 ˜ is covered by two horn speakers.

* McLachlan, , Loud speakers (1934), p. 178, formula 4.Google Scholar

* Loud speakers, p. 183.Google Scholar

* Whittaker, and Watson, , Modern analysis (1920), p. 359.Google Scholar

* The condition ω2 ≫ ¼β2c2 being maintained.

† Loud speakers, p. 335Google Scholar: horn only 4′6″ long, giving small damping below 250 c./s

‡ At abscissa x the sound pressure has the form .

* Loud speakers, pp. 182, 183.Google Scholar

† According to the hypothesis upon which the analysis is based.

‡ Goldstein, and McLachlan, , Wireless Engineer, 11 (1924), 423;Google ScholarJ. Acoue. Soc. Amer. 6 (1935), 275.CrossRefGoogle Scholar