Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T16:44:57.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Transforms which almost vanish at infinity

Published online by Cambridge University Press:  24 October 2008

Louis Pigno
Louis Pigno
Affiliation:
Kansas State University, Manhattan, Kansas
Get access Rights & Permissions [Opens in a new window]

Extract

Let 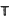be the circle group, M(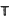) the set of bounded Borel measures on 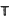and ℤ the additive group of integers. If μ ∈ M(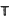) and n ∈ ℤ, define

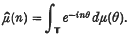
A well-known result of Rajchman states that

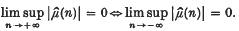
The following quantitative generalization of this result has been given in (2) by K. de Leeuw and Y. Katznelson.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 87 , Issue 1 , January 1980 , pp. 75 - 79
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Davenport, H.On a theorem of P. J. Cohen. Mathematika 7 (1960), 93–97.CrossRefGoogle Scholar
(2)de Leeuw, K. and Katznelson, Y.The two sides of a Fourier-Stieltjes transform and almost idempotent measures. Israel J. Math. 8 (1970), 213–229.CrossRefGoogle Scholar
(3)Gardner, P. and Pigno, L.The two sides of a Fourier-Stieltjes transform. Archiv der Mathematik 32 (1979), 75–78.CrossRefGoogle Scholar
(4)Graham, C. C.Non-Sidon sets in the support of a Fourier-Stieltjes transform. Colloq. Math. 36 (1976), 269–273.CrossRefGoogle Scholar
(5)López, J. M. and Ross, K. A.Sidon Sets (New York, Marcel Dekker).Google Scholar
(6)Pigno, L.Fourier-Stieltjes transforms which vanish at infinity off certain sets. Glasgow Math. J. 19 (1978), 49–56.CrossRefGoogle Scholar
(7)Pigno, L.Small sets in the support of a Fourier-Stieltjes transform. Colloq. Math. (to appear).Google Scholar
(8)Pigno, L. and Smith, B.Almost idempotent measures on compact abelian groups. J. Functional Analysis (to appear).Google Scholar
(9)Pigno, L. and Smith, B. Semi-idempotent and semi-strongly continuous measures. (Submitted.)Google Scholar
(10)Ramsey, L. T. and Wells, B. B.Fourier-Stieltjes transforms of strongly continuous measures. Michigan Math. J. 24 (1977), 13–19.CrossRefGoogle Scholar
(11)Wallen, L. J.Fourier-Stieltjes transforms tending to zero. Proc. Amer. Math. Soc. 24 (1970), 651–652.Google Scholar