Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-11T01:04:38.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Ω theorems for the complex divisor function

Published online by Cambridge University Press:  24 October 2008

R. R. Hall
R. R. Hall
Affiliation:
University of York, Heslington, York, YOl 5DD
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is a sequel to [6] and concerns the complex divisor function

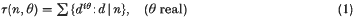
which has had a number of applications in the analytic theory of numbers. Thus Hooley's Δ-function [8] defined by

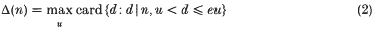
satisfies the inequality

and Erdös' τ+-function, defined by

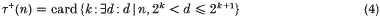
satisfies

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 145 - 157
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bastick, L.. A better lower bound for Σn ≤ xτ+(n). M.Phil thesis (University of York, 1992).Google Scholar
[2]Erdös, P. and Hall, R. R.. The propinquity of divisors. B. London Math. Soc. 11 (1979), 304–307.CrossRefGoogle Scholar
[3]Halberstam, H. and Richert, H.-E.. On a result of R. R. Hall. J. Number Theory, 11 (1979), 76–89.CrossRefGoogle Scholar
[4]Hall, R. R.. Sums of imaginary powers of the divisors of integers. J. London Math. Soc. 9 (1975), 571–580.CrossRefGoogle Scholar
[5]Hall, R. R.. The propinquity of divisors. Acta Arithmetica 49 (1987), 155–163.CrossRefGoogle Scholar
[6]Hall, R. R.. Uniform upper bounds for the complex divisor function. Math. Proc. Cambridge Phil. Soc. 108 (1990), 421–427.CrossRefGoogle Scholar
[7]Hall, R. R. and Tenenbaum, G.. Divisors. Cambridge Tracts in Mathematics No. 90 (Cambridge University Press, 1988).CrossRefGoogle Scholar
[8]Hooley, C.. On a new technique and its applications to the theory of numbers. Proc. London Math. Soc. 38 (1979), 115–151.CrossRefGoogle Scholar
[9]Maier, H. and Tenenbaum, G.. On the set of divisors of an integer. Inventiones Math. 76 (1984), 121–128.CrossRefGoogle Scholar
[10]Tenenbaum, G.. Sur la concentration moyenne des diviseurs. Comment. Math. Helvetici 60 (1985), 411–428.CrossRefGoogle Scholar