Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Benedetto, John J.
1992.
Probabilistic and Stochastic Methods in Analysis, with Applications.
p.
117.
Benedetto, John J.
1992.
Wavelets.
p.
445.
Strichartz, Robert S.
1993.
Characterization of eigenfunctions of the Laplacian by boundedness conditions.
Transactions of the American Mathematical Society,
Vol. 338,
Issue. 2,
p.
971.
Mejjaoli, Hatem
2013.
Spectrum of Functions and Distributions for the Jacobi-Dunkl Transform on $${\mathbb{R}}$$.
Mediterranean Journal of Mathematics,
Vol. 10,
Issue. 2,
p.
753.
Chung, Soon-Yeong
and
Chung, Yun-Sung
2014.
Tempered Gevrey distributions with spectral gaps and their applications.
Integral Transforms and Special Functions,
Vol. 25,
Issue. 2,
p.
85.
Mejjaoli, Hatem
2014.
Spectral theorems associated with the Jacobi–Cherednik operator.
Bulletin des Sciences Mathématiques,
Vol. 138,
Issue. 3,
p.
416.
Andersen, Nils Byrial
2015.
Roe's theorem revisited.
Integral Transforms and Special Functions,
Vol. 26,
Issue. 3,
p.
165.
Andersen, Nils Byrial
2015.
Real Paley–Wiener theorems and Roe's theorem associated with the Opdam–Cherednik transform.
Journal of Mathematical Analysis and Applications,
Vol. 427,
Issue. 1,
p.
47.
Mejjaoli, Hatem
2016.
On the range of the Opdam–Cherednik transform and Roe’s theorem in the Cherednik setting.
Journal of Pseudo-Differential Operators and Applications,
Vol. 7,
Issue. 1,
p.
19.
Mejjaoli, Hatem
2016.
Paley–Wiener Theorems of Generalized Fourier Transform Associated with a Cherednik Type Operator on the Real Line.
Complex Analysis and Operator Theory,
Vol. 10,
Issue. 6,
p.
1145.
Mejjaoli, Hatem
2016.
Spectral theorems associated with the Cherednik operators on $$\mathbb {R}^{d}$$ R d.
Afrika Matematika,
Vol. 27,
Issue. 5-6,
p.
1091.
Mejjaoli, Hatem
2016.
SPECTRAL THEOREMS ASSOCIATED TO THE DUNKL OPERATORS.
Korean Journal of Mathematics,
Vol. 24,
Issue. 4,
p.
693.
Mejjaoli, Hatem
2017.
Paley-Wiener Theorems for the Two-Sided Quaternion Fourier Transform.
Advances in Applied Clifford Algebras,
Vol. 27,
Issue. 2,
p.
1611.
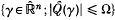 or
or 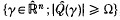 , where
, where 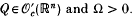 and Ω>0.
and Ω>0.

