Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:17:40.359Z Has data issue: false hasContentIssue false
  • English
  • Français

Tangent sequences in Orlicz and rearrangement invariant spaces

Published online by Cambridge University Press:  24 October 2008

Paweł Hitczenko  and
Stephen J. Montgomery-Smith
Paweł Hitczenko
Affiliation:
Department of Mathematics, Box 8205, North Carolina State University, Raleigh. NC 27695-8205, U.S.A
Stephen J. Montgomery-Smith
Affiliation:
Department of Mathematics, University of Missouri – Columbia, Columbia, MO 65211, U.S.A
Get access Rights & Permissions [Opens in a new window]

Abstract

Let (fn) and (gn) be two sequences of random variables adapted to an increasing sequence of σ-algebras (ℱn) such that the conditional distributions of fn and gn given ℱn coincide. Suppose further that the sequence (gn) is conditionally independent. Then it is known that 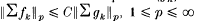where the number C is a universal constant. The aim of this paper is to extend this result to certain classes of Orlicz and rearrangement invariant spaces. This paper includes fairly general techniques for obtaining rearrangement invariant inequalities from Orlicz norm inequalities.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 1 , January 1996 , pp. 91 - 101
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arazy, J. and Cwikiel, M.. A new characterization of the interpolation spaces between Lp and Lq. Math. Scand. 55 (1984), 253–270.CrossRefGoogle Scholar
[2]Burkholder, D. L.. Distribution function inequalities for martingales. Ann. Probab. 1 (1973), 19–42.CrossRefGoogle Scholar
[3]Garling, D. J. H.. Random martingale transform inequalities. Probability in Banach spaces, 6 (Sandbjerg, Denmark, 1986). Progr. Prob. Statist. 20 (1990), 101–119.Google Scholar
[4]Hitczenko, P.. Comparison of moments for tangent sequences of random variables. Probab. Theory Related Fields 78 (1988), 223–230.CrossRefGoogle Scholar
[5]Hitczenko, P.. Domination inequality for martingale transforms of a Rademacher sequence. Israel J. Math. 84 (1993), 161–178.CrossRefGoogle Scholar
[6]Hitczenko, P.. On a domination of sums of random variables by sums of conditionally independent ones. Ann. Probab. 22 (1994), 453–468.CrossRefGoogle Scholar
[7]Johnson, W. B. and Schechtman, G.. Martingale inequalities in rearrangement invariant function spaces. Israel J. Math. 64 (1988), 267–275.Google Scholar
[8]Klass, M. J.. A best possible improvement of Wald's equation. Ann. Probab. 16 (1988), 840–853.CrossRefGoogle Scholar
[9]Kwapień, S.. Decoupling inequalities for polynomial chaos. Ann. Probab. 15 (1987), 1062–1072.CrossRefGoogle Scholar
[10]Kwapień, S. and Woyczyński, W. A.. Semimartingale integrals via decoupling inequalities and tangent processes. Probab. Math. Statist. 12 (1991), 165–200.Google Scholar
[11]Kwapień, S. and Woyczyński, W. A.. Random series and stochastic integrals. Single and multiple (Birkhäuser, 1992).CrossRefGoogle Scholar
[12]Ledoux, M. and Talagrand, M.. Probability in Banach spaces (Springer, 1991).CrossRefGoogle Scholar
[13]Lindenstrauss, J. and Tzafriri, L.. Classical Banach spaces. Function spaces (Springer, 1977).Google Scholar
[14]Montgomery-Smith, S. J.. Comparison of Orlicz-Lorentz spaces. Studia Math. 103 (1992), 161–189.CrossRefGoogle Scholar