Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T16:47:54.993Z Has data issue: false hasContentIssue false
  • English
  • Français

Tables for numerical integration at non-equidistant argument steps

Published online by Cambridge University Press:  24 October 2008

H. O. Hartley
H. O. Hartley
Affiliation:
University CollegeLondon
Get access Rights & Permissions [Opens in a new window]

Extract

1. Published tables facilitating the numerical evaluation of the definite integral

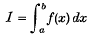
from given numerical values f(xi) of the integrand in the form of a weighted sum

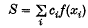
essentially deal with the following situations:

(a) The arguments xi are equidistant, i.e. xi = x0+iw; i=integer and the weight coefficients ci are tabulated for all arguments xi occurring in the summation. Among these tables the most important are:

(a1) panels in which the end-points of the integration a and b are two of the xi, and in particular

(a11) panels confined to the range of the integration in which

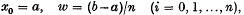
(a12) panels extending beyond the range of integration which usually have the same number of arguments, k, below a and beyond b, so that

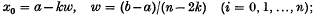
(a2) panels in which a and b are at distance ½w from one of the xi, and in particular

(a21) panels confined to the range of integration in which

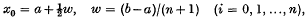
(a22) panels extending beyond the range of integration which usually have the same number of (k) points below a and beyond b, so that

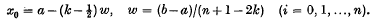
(b) The n arguments xi are not equidistant but are specially chosen so that for a given n the sum S approximates to I with highest precision. Gauss's formula (see, for example, Milne-Thomson (4)) and various formulae of approximate product integration (see, for example, Beard (l)) are examples of these. In Chebyshev's integration formula (see, for example, Runge and König (5)) the xi required for equal weights ctare used, resulting in an important formula when the ordinates f(xi) are affeected by observational errors of equal variance.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 3 , July 1952 , pp. 436 - 442
Copyright
Copyright © Cambridge Philosophical Society 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Beard, R. E.Some notes on approximate product integration. J. Inst. Actu. 73 (1947), 356.CrossRefGoogle Scholar
(2)Comrie, L. J.Chambers's six-figure mathematical tables, vol. 2 (Edinburgh, 1949).Google Scholar
(3)Fletcher, A., Miller, J. C. P. and Rosenhead, L.An index of mathematical tables (London, 1946).Google Scholar
(4)Milne-Thomson, L. M.The calculus of finite differences (London, 1933).Google Scholar
(5)Runge, C. and König, H.Vorlesungen über numerisches Rechnen (Berlin, 1924), p. 272.CrossRefGoogle Scholar