Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Graham, Colin C.
2008.
The support of tempered distributions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 144,
Issue. 2,
p.
495.
Bowers, Adam
2014.
A Radon–Nikodým theorem for Fréchet measures.
Journal of Mathematical Analysis and Applications,
Vol. 411,
Issue. 2,
p.
592.


 with support in the closed set
with support in the closed set 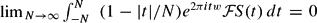 uniformly for
uniformly for 