Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:40:38.276Z Has data issue: false hasContentIssue false
  • English
  • Français

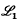The supersolvable residual of an -group

Published online by Cambridge University Press:  24 October 2008

Ben Brewster  and
Malcolm Ottaway
Ben Brewster
Affiliation:
State University of New York at Binghamton, New York 13901
Malcolm Ottaway
Affiliation:
State University of New York at Binghamton, New York 13901
Get access Rights & Permissions [Opens in a new window]

Extract

Let 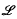be the class of groups possessing a subgroup of index n for each divisor n of the group order. McLain (7) initiated the formal investigation of 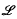and observed that every solvable group is a direct factor of an 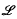-group. However, subclasses of 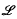provide some interesting problems. Various subclasses of 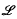which satisfy other properties were studied by McLain; the upshot being that these classes approach supersolvability. This program was pursued by Humphreys (3) and Humphreys and Johnson (4), among others. In particular, 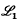, the largest quotient closed subclass of 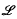, was considered in (3) and (4). Humphreys (3) has shown an odd order 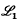-group is supersolvable, but provides some non-supersolvable 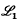groups. Our motivation is that if S ∈ QR0(S3), the formation generated by S3, and V is a faithful irreducible GF(2) [S]-module, the semidirect product VS ∈ .

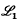Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 80 , Issue 3 , November 1976 , pp. 447 - 450
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Alperin, J. L.Large abelian subgroups of p-groups. Trans. Amer. Math. Soc. 117 (1965), 10–20.Google Scholar
(2)Dixon, J. D.The structure of linear groups (London; Van Nostrand Reinhold Company, 1971).Google Scholar
(3)Humphreys, J. F.On groups satisfying the converse to Lagrange's Theorem. Proc. Cambridge Philos. Soc. 75 (1974), 25–32.CrossRefGoogle Scholar
(4)Humphreys, J. F. & Johnson, D. L.On Lagrangian Groups. Trans. Amer. Math. Soc. 180 (1973), 291–300.CrossRefGoogle Scholar
(5)Huppert, B.Lineare auflobare Gruppen. Math. Zeit. 67 (1957), 479–518.CrossRefGoogle Scholar
(6)Huppert, B.Endliche Gruppen I. (Berlin, Heidelberg, New York; Springer-Verlag, 1967).CrossRefGoogle Scholar
(7)McLain, D. H.The existence of subgroups of given order in finite groups. Proc. Cambridge Philos. Soc. 53 (1957), 278–285.CrossRefGoogle Scholar
(8)Rotman, J. J.The theory of groups; an introduction. Second edition (Boston; Allyn and Bacon, Inc., 1973).Google Scholar