Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T15:07:44.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Summability of Hermite polynomial expansions of generalized functions

Published online by Cambridge University Press:  24 October 2008

Z. Ditzian
Z. Ditzian
Affiliation:
University of Alberta, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

1. Introduction: The well-known result that every function f(x) ∈ L2(–∞, ∞) can be expanded in L2(– ∞,∞) by where 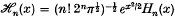and was recently followed by an expansion theorem for generalized functions. In papers by Wildlund(8), Giertz(4) and Zemanian(9) it was shown that a tempered distribution f∈S′ can be expanded by Hermite functions that is

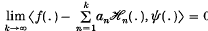
for all ψ∈S (the space of rapidly decreasing test functions).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 1 , July 1970 , pp. 129 - 139
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bilodeau, G. G.On the summability of series of Hennite polynomials. J. Math. Anal. Appl. 8 (1964), 406–422.CrossRefGoogle Scholar
(2)Hirschmann, I. I. and Widder, D. V.The Convolution Transform. (Princeton University Press, 1955).Google Scholar
(3)Gelfand, I. M. and Shilov, G. E.Generalized Functions. Vol. 2. (English translation, Academic Press, 1968.)Google Scholar
(4)Giebtz, M.On the expansion of certain generalized functions of series of orthogonal func-tions. Proc. London Math. Soc. (3), 14 (1964), 45–52.Google Scholar
(5)Korevaar, J.Pansion and the theory of Fourier transforms Trans. Amer. Math. Soc. 31 (1959), 53–101.CrossRefGoogle Scholar
(6)Sansone, G.Orthogonal functions (Interscience, New York, 1959).Google Scholar
(7)Szego, G.Orthogonal polynomials. Amer. Math. Soc. Colloq. Publ. Vol. XXIII (New York, 1959).Google Scholar
(8)Widlund, O.On the expansion of generalized functions in series of Hermite functions. Kungl. Tekn. Högsk. Handl. Stockholm 173 (1961).Google Scholar
(9)Zemanian, A.Orthonormal Series Expansions of certain Distributions and Transform calculus. J. Math. Anal. Appl. 14 (1966), 263–275.CrossRefGoogle Scholar
(10)Zemanian, A.A generalized Weierstrass transformation. SIAM J. Appl. Math. 15 (1967), 1088–1105.CrossRefGoogle Scholar
(11)Zemanian, A.Generalized integral transformation with Applications (Interscience, 1968).Google Scholar