Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T01:57:00.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Sufficient Statistics and Orthogonal Parameters

Published online by Cambridge University Press:  24 October 2008

Ann F. S. Mitchell
Ann F. S. Mitchell
Affiliation:
The Statistical LaboratoryCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let 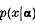be, for a set of n real continuous parameters 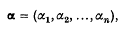the probability density function of a random variable x with respect to a σ-finite measure μ on a σ-algebra of subsets of the sample space 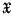. If x; is a continuous random variable, μ will be Lebesgue measure on the Borel sets of a Euclidean sample space and, if x is discrete, μ will be counting measure on the class of all sets of a countable sample space. The parameters αi are said to be orthogonal (Jeffreys (3), pp. 158,184) if .

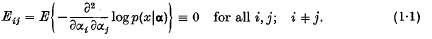Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 326 - 337
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Huzurbazar, V. SProc. Cambridge Philos. Soc. 46 (1950), 281–284.CrossRefGoogle Scholar
(2)Huzurbazar, V. SSankhyā, 17 (1956), 217–220.Google Scholar
(3)Jeffreys, H.Theory of probability, 2nd ed. (Oxford, 1948).Google Scholar
(4)Jeffreys, H.Proc. Cambridge Philoa. Soc. 56 (1960), 393–395.Google Scholar
(5)Koopman, B. OTrans. American Math. Soc. 39 (1936), 399–409.CrossRefGoogle Scholar
(6)Lehmann, E. LTesting statistical hypotheses (New York, 1959).Google Scholar