No CrossRef data available.
Article contents
Stochastic independence in non-commutative probability theory
Published online by Cambridge University Press: 24 October 2008
Abstract
For a family {Xα} of random variables over a probability space 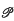 , stochastic independence can be formulated in terms of factorization properties of characteristic functions. This idea is reformulated for a family {Aα} of selfadjoint operators over a probability gage space
, stochastic independence can be formulated in terms of factorization properties of characteristic functions. This idea is reformulated for a family {Aα} of selfadjoint operators over a probability gage space 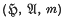 and is shown to be inappropriate as a non-commutative generalization. Indeed, such factorization properties imply that the {Aα} mutually commute and are versions of independent random variables in the usual sense.
and is shown to be inappropriate as a non-commutative generalization. Indeed, such factorization properties imply that the {Aα} mutually commute and are versions of independent random variables in the usual sense.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 1 , July 1979 , pp. 103 - 114
- Copyright
- Copyright © Cambridge Philosophical Society 1979


