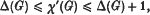Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chetwynd, A. G.
and
Hilton, A. J. W.
1986.
Critical star multigraphs.
Graphs and Combinatorics,
Vol. 2,
Issue. 1,
p.
209.
Hilton, A. J. W.
and
Johnson, P. D.
1987.
Graphs which are vertex-critical with respect to the edge-chromatic number.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 102,
Issue. 2,
p.
211.
Chetwynd, A.G.
and
Hilton, A.J.W.
1988.
Graph Theory in Memory of G.A. Dirac.
Vol. 41,
Issue. ,
p.
91.
Hilton, A. J. W.
and
Johnson, P. D.
1989.
Graphs which are vertex‐critical with respect to the edge‐chromatic class.
Mathematika,
Vol. 36,
Issue. 2,
p.
241.
Hilton, A.J.W.
1989.
Graph Colouring and Variations.
Vol. 39,
Issue. ,
p.
61.
Hilton, A.J.W.
1989.
Two conjectures on edge-colouring.
Discrete Mathematics,
Vol. 74,
Issue. 1-2,
p.
61.
Niessen, Thomas
and
Volkmann, Lutz
1990.
Class 1 conditions depending on the minimum degree and the number of vertices of maximum degree.
Journal of Graph Theory,
Vol. 14,
Issue. 2,
p.
225.
Plantholt, Michael J.
and
Tipnis, Shailesh K.
1990.
The chromatic index of multigraphs that are nearly full.
Discrete Mathematics,
Vol. 82,
Issue. 2,
p.
197.
Hilton, A.J.W.
1993.
Recent results on the total chromatic number.
Discrete Mathematics,
Vol. 111,
Issue. 1-3,
p.
323.
1994.
Graph Coloring Problems.
p.
190.
Ortiz Z., Carmen
and
Villanueva-Ilufi, Mónica
2004.
Difficult Problems in Threshold Graphs.
Electronic Notes in Discrete Mathematics,
Vol. 18,
Issue. ,
p.
187.
Plantholt, Michael
2004.
Overfull conjecture for graphs with high minimum degree.
Journal of Graph Theory,
Vol. 47,
Issue. 2,
p.
73.
De Simone, Caterina
and
de Mello, C.P.
2006.
Edge-colouring of join graphs.
Theoretical Computer Science,
Vol. 355,
Issue. 3,
p.
364.
Plummer, Michael D.
2007.
Graph factors and factorization: 1985–2003: A survey.
Discrete Mathematics,
Vol. 307,
Issue. 7-8,
p.
791.
De Simone, Caterina
and
Galluccio, Anna
2008.
Combinatorial Optimization and Applications.
Vol. 5165,
Issue. ,
p.
351.
Cariolaro, David
2009.
A theorem in edge colouring.
Discrete Mathematics,
Vol. 309,
Issue. 12,
p.
4208.
Morais de Almeida, Sheila
Picinin de Mello, Célia
and
Morgana, Aurora
2012.
On the classification problem for split graphs.
Journal of the Brazilian Computer Society,
Vol. 18,
Issue. 2,
p.
95.
de Figueiredo, Celina M.H.
2012.
The P versus NP–complete dichotomy of some challenging problems in graph theory.
Discrete Applied Mathematics,
Vol. 160,
Issue. 18,
p.
2681.
Luo, Rong
and
Zhao, Yue
2013.
A Sufficient Condition for Edge Chromatic Critical Graphs to Be Hamiltonian—An Approach to Vizing's 2‐Factor Conjecture.
Journal of Graph Theory,
Vol. 73,
Issue. 4,
p.
469.
Ghorbani, Modjtaba
2013.
Remarks on Extremal Overfull Graphs.
Applied Mathematics,
Vol. 04,
Issue. 08,
p.
1106.
 , where
, where  is a set of colours and E(G) is the set of edges of G, such that no two edges receiving the same colour have a vertex in common. The chromatic index, or edge-chromatic numberχ′(G) of G is the least value of |
is a set of colours and E(G) is the set of edges of G, such that no two edges receiving the same colour have a vertex in common. The chromatic index, or edge-chromatic numberχ′(G) of G is the least value of | | for which an edge-colouring of G exists. Generalizing a well-known theorem of Vizing [14], we showed in [6] that, for a star-multigraph G,
| for which an edge-colouring of G exists. Generalizing a well-known theorem of Vizing [14], we showed in [6] that, for a star-multigraph G,