Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T01:27:10.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Some theorems in the metric theory of diophantine approximation

Published online by Cambridge University Press:  24 October 2008

Glyn Harman
Glyn Harman
Affiliation:
University College, Cardiff
Get access Rights & Permissions [Opens in a new window]

Extract

An excellent introduction to the metric theory of diophantine approximation is provided by [19], where, in chapter 1·7, the reader may find a discussion of the first two problems considered in this paper. Our initial question concerns the number of solutions of the inequality

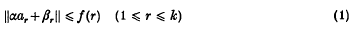
for almost all α(in the sense of Lebesgue measure on ℝ). Here ∥ ∥ denotes distance to a nearest integer, {βr}, {ar} are given sequences of reals and distinct integers respectively, and f is a function taking values in [0, ½] and with Σf(r) divergent (for convenience we write ℱ for the set of all such functions). It is reasonable to expect that, for almost all α and with some additional constraint on f, the number of solutions of (1) is asymptotically equal to

as k tends to infinity.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 3 , May 1986 , pp. 385 - 394
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baker, R. C.. Riemann sums and Lebesgue integrals. Quart. J. Math. Oxford Ser. (2) 27 (1976), 191–198.CrossRefGoogle Scholar
[2]Baker, R. C.. On numbers with many rational approximations. Math. Proc. Cambridge Philos. Soc. 86 (1979), 25–27.CrossRefGoogle Scholar
[3]Baker, R. C.. Metric number theory and the large sieve. J. London Math. Soc. (2) 24 (1981), 34–40.CrossRefGoogle Scholar
[4]Cassels, J. W. S.. Some metrical theorems in Diophantine approximation. Proc. Cambridge Philos. Soc. 46 (1950), 209–218.CrossRefGoogle Scholar
[5]Duffin, R. J. and Schaeffer, A. C.. Khintchine's problem in metric diophantine approximation. Duke Math. J. 8 (1941), 243–255.CrossRefGoogle Scholar
[6]Dyer, T. and Harman, G.. Sums involving common divisors. (In the Press.)Google Scholar
[7]Ennola, V.. On metric diophantine approximation. Ann. Univ. Turku. Ser. A I (1967), No. 113.Google Scholar
[8]Erdös, P.. On the strong law of large numbers. Trans. Amer. Math. Soc. 67 (1949), 51–56.CrossRefGoogle Scholar
[9]Gál, I. S. and Koksma, J. F.. Sur l'ordre de grandeur des functions sommables. Proc. Kon. Ned. Akad. Weten. 53 (1950), 638–653.Google Scholar
[10]Gallagher, P. X.. Metric simultaneous Diophantine approximation. II. Mathematika 12 (1965), 123–127.CrossRefGoogle Scholar
[11]Jessen, B.. On the approximation of Lebesgue integrals by Riemann sums. Ann. Math. (2) 35 (1934), 248–251.CrossRefGoogle Scholar
[12]Koksma, J. F.. On sequences (λnx) and functions g(t) ∈ L2. J. Math. Pures et Appl. 35 (1956), 289–296.Google Scholar
[13]Koksma, J. F.. Eon algemeene stelling uit de theorie der gelijkmatige verdeeling modulo 1. Mathematica (Zutphen B) 11 (1942–1943), 7–11.Google Scholar
[14]Koksma, J. F.. An arithmetical property of some summable functions. Proc. Kon. Ned. Akad. Weten. 53 (1952), 959–972.Google Scholar
[15]Le Veque, W. J.. On the frequency of small fractional parts in certain real sequences. III. J. reine angew. Math. 202 (1959), 215–220.CrossRefGoogle Scholar
[16]Le Veque, W. J.. On the frequency of small fractional parts in certain real sequences. IV. Acta Arithmetica 31 (1976), 231–237.CrossRefGoogle Scholar
[17]Schmidt, W. M.. A metrical theorem in Diophantine approximation. Canad. J. Math. 12 (1960), 619–631.CrossRefGoogle Scholar
[18]Schmidt, W. M.. Metrical theorems on fractional parts of sequences. Trans. Amer. Math. Soc. 110 (1964), 493–518.CrossRefGoogle Scholar
[19]Sprindzuk, V. G.. Metric theory of Diophantine approximations, translated by Silverman, R. A. (Winston/Wiley, 1979).Google Scholar