Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-02T22:22:38.329Z Has data issue: false hasContentIssue false
  • English
  • Français

Some formulae of P. Stein and others concerning trigonometrical sums

Published online by Cambridge University Press:  24 October 2008

N. B. Slater
N. B. Slater
Affiliation:
University of Leeds
Get access Rights & Permissions [Opens in a new window]

Extract

Let

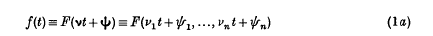
where the frequencies vr are strictly positive and the amplitudes ar are non-zero; and let

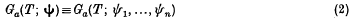
be the number of zeros of f(t) – a for 0 ≤ t < T. In physical problems, where f(t) may represent, for example, a general coordinate in a vibrating dynamical system or a set of alternating currents in a cable, formulae are required for the frequency with which f(t) passes through a given value a; that is, for asymptotic or average values of Ga/T. The purpose here is to collect such formulae, and to sketch their background and relations in a way which may suggest extensions. The writer is particularly indebted to Prof. P. Stein for a manuscript containing new results (SI-V in §§2 and 5 below) and for his permission to publish them without his original proofs; these proofs were extensions of the method he gave (6) for the case n = 2.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 1 , January 1954 , pp. 33 - 39
Copyright
Copyright © Cambridge Philosophical Society 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Kac, M.Amer. J. Math. 65 (1943), 609. (See also some corrigenda in Proc. Land. math. Soc. (2), 50 (1949), 390.)CrossRefGoogle Scholar
(2)Kac, M., Van Kampen, E. R. and Wintner, A.Amer. J. Math. 61 (1939), 985.CrossRefGoogle Scholar
(3)Slater, N. B.Proc. Camb. phil. Soc. 35 (1939), 67.CrossRefGoogle Scholar
(4)Slater, N. B.Proc. roy. Soc. A, 194 (1948), 112.Google Scholar
(5)Slater, N. B.Phil. Trans. A, 246 (1953), 57.Google Scholar
(6)Stein, P.Proc. Camb. phil. Soc. 31 (1935), 455.CrossRefGoogle Scholar