Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T07:28:39.137Z Has data issue: false hasContentIssue false
  • English
  • Français

Small sets containing any pattern

Published online by Cambridge University Press:  31 July 2018

URSULA MOLTER  and
ALEXIA YAVICOLI
URSULA MOLTER
Affiliation:
Departamento de Matemática and IMAS/UBA-CONICET, Facultad de Cs. Exactas y Naturales, Universidad de Buenos Aires, Ciudad Universitaria, Pab. I, (1428) CABA, Argentina. e-mail: [email protected]; [email protected]
ALEXIA YAVICOLI
Affiliation:
Departamento de Matemática and IMAS/UBA-CONICET, Facultad de Cs. Exactas y Naturales, Universidad de Buenos Aires, Ciudad Universitaria, Pab. I, (1428) CABA, Argentina. e-mail: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given any dimension function h, we construct a perfect set E ⊆ 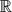${\mathbb{R}}$ of zero h-Hausdorff measure, that contains any finite polynomial pattern.

This is achieved as a special case of a more general construction in which we have a family of functions 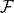$\mathcal{F}$ that satisfy certain conditions and we construct a perfect set E in 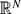${\mathbb{R}}^N$, of h-Hausdorff measure zero, such that for any finite set {f1,. . .,fn} ⊆ 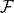$\mathcal{F}$, E satisfies that 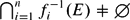$\bigcap_{i=1}^n f^{-1}_i(E)\neq\emptyset$.

We also obtain an analogous result for the images of functions. Additionally we prove some related results for countable (not necessarily finite) intersections, obtaining, instead of a perfect set, an 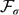$\mathcal{F}_{\sigma}$ set without isolated points.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 168 , Issue 1 , January 2020 , pp. 57 - 73
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†The research for this paper was partially supported by grants UBACyT 2014-2017 20020130100403BA, PIP 11220110101018 (CONICET) and PICT 2014 - 1480, MinCyT.

References

REFERENCES

[1] Bergelson, V. and Leibman, A. Polynomial extensions of van der Waerden's and Szemerédi's theorems. J. Amer. Math. Soc. 9 (3)(1996), 725–753.Google Scholar
[2] Boshernitzan, M. and Chaika, J. Dichotomy for Arithmetic Progressions in subsets of reals. Proc. Amer. Math. Soc. 144 (12) (2016), 5029–5034.Google Scholar
[3] Chan, V., Łaba, I. and Pramanik, M. Finite configurations in sparse sets. J. Anal. Math. 128 (2016), 289–335.Google Scholar
[4] Darji, U.B. and Keleti, T. Covering ${\mathbb{R}}$ with translates of a compact set. Proc. Amer. Math. Soc. 131 (8) (2003), 2598–2596Google Scholar
[5] Davies, R.O., Marstrand, J.M. and Taylor, S.J. On the intersections of transforms of linear sets. Colloq. Math. 7 (1959/1960), 237–243.Google Scholar
[6] Erdős, P. Remarks on some problems in number theory Math. Balkanica 4 (1974), 197–202.Google Scholar
[7] Falconer, K. J. On a problem of Erdős on sequences and measurable sets. Proc. Amer. Math. Soc 90 (1984), 77–78.Google Scholar
[8] Falconer, K. J. On a problem of Erdős on fractal combinatorial geometry. J. Combin. Theory Ser. A 59 (1) (1992), 142–148.Google Scholar
[9] Fraser, R. and Pramanik, M. Large sets avoiding patterns Anal. PDE 11 (5) (2018), 1083–1011.Google Scholar
[10] Furstenberg, H.. Recurrence in ergodic theory and combinatorial number theory. (Princeton University Press, Princeton, N.J., m. B. Porter Lectures, 1981).Google Scholar
[11] Henriot, K., Łaba, I. and Pramanik, M. On polynomial configurations in fractal sets. Anal. PDE 9 (5) (2016), 1153–1184.Google Scholar
[12] Iosevich, A. and Liu, B.. Equilateral triangles in subsets of R d of large hausdorff dimension. Preprint, arXiv:1603.01907 (2016).Google Scholar
[13] Łaba, I. and Pramanik, M. Arithmetic progressions in sets of fractional dimension. Geom. Funct. Anal. 19 (2009), 429–456.Google Scholar
[14] Keleti, T. Construction of one-dimensional subsets of the reals not containing similar copies of given patterns. Anal. PDE 1 (1) (2008), 29–33.Google Scholar
[15] Keleti, T., Nagy, D.T. and Shmerkin, P. Squares and their centers. J. Anal. Math. 134 (2) (2014), 643–669.Google Scholar
[16] Maga, P. Full dimensional sets without given patterns. Real Anal. Exchange 36 (1) (2010/2011), 79–90.Google Scholar
[17] Máthé, A. Sets of large dimension not containing polynomial configurations. Avd. Math. 316 (2017), 691–709.Google Scholar
[18] Szemerédi, E. On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 (1975), 199–245, collection of articles in memory of Juriĭ Vladimirovič Linnik.Google Scholar
[19] Tao, T. and Ziegler, T. The primes contain arbitrarily long polynomial progressions. Acta Math. 201 (2008), 213–305.Google Scholar
[20] Tao, T. and Ziegler, T. Polynomial Patterns in the Primes. Forum Math. Pi 6 (e1) (2018), 60pp.Google Scholar
[21] Yavicoli, A. Large sets avoiding linear patterns. Proc. Amer. Math. Soc. To appear (2017).Google Scholar