Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T10:40:28.103Z Has data issue: false hasContentIssue false
  • English
  • Français

Singularities of convex-polygonally generated shape-densities

Published online by Cambridge University Press:  24 October 2008

Hui-Lin Le
Hui-Lin Le
Affiliation:
Darwin College, University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Abstract

In earlier papers Kendall and Le[3,4] made a geometrical study of the structure and singularities of a convex-polygonally generated shape-density 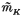for any convex polygon K. The present work describes the singular tessellation T(K) in algebraic terms, and obtains explicit formulae for the ‘jump functions’ of m̃ across every edge of the tessellation. These results, combined with earlier work by Le[5] on the basic tile, make it possible to find m̃ explicitly in every tile by what we have called the ‘stepping-stone’ method. In a closing section the exact order of the differential singularity is found at the tile boundaries.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 587 - 596
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Kendall, D. G.. Shape-manifolds, procrustean metrics, and complex projective spaces. Bull. London Math. Soc. 16 (1984), 81–121.Google Scholar
[2]Kendall, D. G.. Exact distributions for shapes of random triangles in convex sets. Adv. in Appl. Probab. 17 (1985), 308–329.CrossRefGoogle Scholar
[3]Kendall, D. G. and Le, H.-L.. Exact shape-densities for random triangles in convex polygons. Analytic and Geometric Stochastics (Special Supplement to Adv. in Appl. Probab., (1986) 59–72.Google Scholar
[4]Kendall, D. G. and Le, H.-L.. The structure and explicit determination of convex-polygonally generated shape-densities on . Adv. in Appl. Probab. (to appear).Google Scholar
[5]Le, H.-L.. Explicit formulae for polygonally generated shape-densities in the basic tile. Math. Proc. Cambridge Philos. Soc. 101 (1987), 313–321.CrossRefGoogle Scholar