Singular n-tuples and Hausdorff dimension

Extract

1. Introduction. Throughout the paper θ = (θ₁, …, θ_n), φ = (φ₁, …, φ_n), … denote points of Euclidean space R_n. We write K_n for the set of θ in R_n for which θ_l, …, θ_n, 1 are linearly independent over the rational numbers. We denote points of the set of integer n-tuples Z_n by x, y, … We write

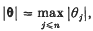
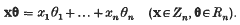
If α is a real number, ∥α∥ denotes the distance from α to the nearest integer.

Let θ ∈ R_n. By a theorem of Dirichlet ((2), chapter 1, theorem VI).

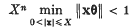
for all X ≥ 1. We say that θ is singular if

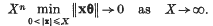
Singular points form a set of n-dimensional Lebesgue measure zero. In fact, H. Davenport and W. M. Schmidt (3) showed that

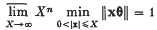
for almost all θ in R_n. Although there are no singular numbers in K_l ((2), p. 94) there are ‘highly singular’ n-tuples in K_n for n ≥ 2.