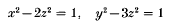Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bennett, Michael A.
1996.
Solving Norm Form Equations Via Lattice Basis Reduction.
Rocky Mountain Journal of Mathematics,
Vol. 26,
Issue. 3,
Bennett, Michael A.
1997.
Effective measures of irrationality for certain algebraic numbers.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 62,
Issue. 3,
p.
329.
Wakabayashi, Isao
1997.
On a Family of Quartic Thue Inequalities I.
Journal of Number Theory,
Vol. 66,
Issue. 1,
p.
70.
Katayama, Shin-ichi
Levesque, Claude
and
Nakahara, Toru
1999.
On the units and the class numbers of certain composita of two quadratic fields.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 75,
Issue. 4,
Wakabayashi, Isao
2000.
On a Family of Quartic Thue Inequalities, II.
Journal of Number Theory,
Vol. 80,
Issue. 1,
p.
60.
Wakabayashi, Isao
2002.
Analytic Number Theory.
Vol. 6,
Issue. ,
p.
359.
Wakabayashi, Isao
2002.
Cubic Thue inequalities with negative discriminant.
Journal of Number Theory,
Vol. 97,
Issue. 2,
p.
222.
TANAKA, Yuzen
2003.
RATIONAL APPROXIMATIONS OF (1 + x)a AND APPLICATIONS TO THUE INEQUALITIES.
Kyushu Journal of Mathematics,
Vol. 57,
Issue. 2,
p.
277.
Ziegler, Volker
2006.
On a family of relative quartic Thue inequalities.
Journal of Number Theory,
Vol. 120,
Issue. 2,
p.
303.
JADRIJEVIĆ, BORKA
and
ZIEGLER, VOLKER
2006.
A SYSTEM OF RELATIVE PELLIAN EQUATIONS AND A RELATED FAMILY OF RELATIVE THUE EQUATIONS.
International Journal of Number Theory,
Vol. 02,
Issue. 04,
p.
569.
Wakabayashi, Isao
2007.
Number of solutions for cubic Thue equations with automorphisms.
The Ramanujan Journal,
Vol. 14,
Issue. 1,
p.
131.
Fujita, Yasutsugu
2008.
The extensibility of Diophantine pairs{k−1,k+1}.
Journal of Number Theory,
Vol. 128,
Issue. 2,
p.
322.
Fujita, Yasutsugu
2009.
Any Diophantine quintuple contains a regular Diophantine quadruple.
Journal of Number Theory,
Vol. 129,
Issue. 7,
p.
1678.
He, B.
and
Togbé, A.
2009.
On a family of diophantine triples {k, A 2 k + 2A, (A + 1)2 k + 2 (A + 1)} with two parameters.
Acta Mathematica Hungarica,
Vol. 124,
Issue. 1-2,
p.
99.
Filipin, Alan
2009.
On the Size of Sets in Which $xy + 4$ is Always a Square.
Rocky Mountain Journal of Mathematics,
Vol. 39,
Issue. 4,
Fujita, Yasutsugu
2009.
Extensions of the D(∓k 2)-triples {k 2, k 2 ± 1, 4k 2 ± 1}.
Periodica Mathematica Hungarica,
Vol. 59,
Issue. 1,
p.
81.
WAKABAYASHI, ISAO
2012.
NUMBER OF SOLUTIONS FOR QUARTIC SIMPLE THUE EQUATIONS.
International Journal of Number Theory,
Vol. 08,
Issue. 06,
p.
1367.
Filipin, Alan
and
Baćić, Ljubica
2013.
D(4)-pair and its extension.
Electronic Notes in Discrete Mathematics,
Vol. 43,
Issue. ,
p.
31.
Saradha, N.
and
Sharma, Divyum
2015.
Simultaneous rational approximation via Rickert’s integrals.
Indagationes Mathematicae,
Vol. 26,
Issue. 1,
p.
88.
Cipu, Mihai
and
Fujita, Yasutsugu
2015.
Bounds for Diophantine quintuples.
Glasnik Matematicki,
Vol. 50,
Issue. 1,
p.
25.
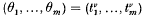 for rational t1, …, tm, v. If t1, …, tm, are sufficiently close to 1 with respect to a common denominator we shall derive an effective inequality of the form max {|θ1 – p1 / q|, …, |θm – pm / q|} > cq–1–λ for all integers p1, …, pm, q with q > 0. The technique is used to derive the inequality
for rational t1, …, tm, v. If t1, …, tm, are sufficiently close to 1 with respect to a common denominator we shall derive an effective inequality of the form max {|θ1 – p1 / q|, …, |θm – pm / q|} > cq–1–λ for all integers p1, …, pm, q with q > 0. The technique is used to derive the inequality